du vil måske gerne læse Introduktion til Integration først!

Integration

Integration kan bruges til at finde områder, volumener, centrale punkter og mange nyttige ting. Men det bruges ofte til at finde området under grafen for en funktion som denne:
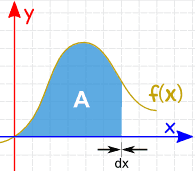
området kan findes ved at tilføje skiver, der nærmer sig nul i bredden: og der er regler for Integration, der hjælper os med at få svaret.

Notation

symbolet for “integral” er en stilfuld “s” (for “sum”, ideen om opsummering af skiver):

efter det integrerede symbol sætter vi den funktion, vi vil finde integralet af (kaldet integranden).

og slut derefter af med DKs for at betyde, at skiverne går i h-retningen (og nærmer sig nul i bredden).

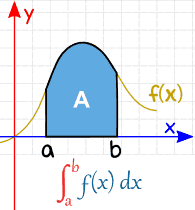
Definite Integral

en bestemt Integral har start-og slutværdier: med andre ord er der et interval .

a og b (kaldet grænser, grænser eller grænser) sættes nederst og øverst på “S”, som dette:

Definite Integral (from a to b)		Indefinite Integral (no specific values)

We find the Definite Integral by calculating the Indefinite Integral at a, and at b, then subtracting:

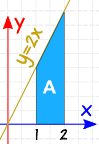
eksempel: hvad er 2 til 1 2 gange DH

Vi bliver bedt om det bestemte Integral, fra 1 til 2, af 2 gange DH

først skal vi finde det ubestemte integreret.

Ved hjælp af Integrationsreglerne finder vi, at vi nu beregner det ved 1, og 2:

• ved 1: 2 gange D = 12 + C
• ved 2: 2 gange D=22 + C

trækker fra:

(22 + C) − (12 + C)

22 + C − 12 − C

4 − 1 + C − c = 3

og “C” bliver annulleret … så med bestemte integraler kan vi ignorere C.

resultat:

2

1

2 gange D = 3

kontroller: med en så enkel form, lad os også prøve at beregne området efter geometri:

a = 2+42 × 1 = 3

Ja, Det har et område på 3.

(Yay!)

Notation: Vi kan vise det ubestemte integral (uden +C) inde i firkantede parenteser, med grænserne A og b efter, som dette:

eksempel (fortsat)

en god måde at vise dit svar på:

2

1

2

=

2

1

=22 − 12

= 3

lad os prøve et andet eksempel:

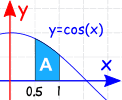
Example:

The Definite Integral, from 0.5 to 1.0, of cos(x) dx:

1

∫

0.5

cos(x) dx

(Note: x must be in radians)

The Indefinite Integral is: ∫cos(x) dx = sin(x) + C

We can ignore C for definite integrals (as we saw above) and we get:

1

∫

0.5

cos(x) dx

=

1

0.5

= sin(1) − sin(0.5)

= 0.841… − 0.479…

= 0.362…

And another example to make an important point:

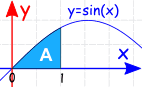
Example:

The Definite Integral, from 0 to 1, of sin(x) dx:

1

0

den ubestemte Integral er:) + c

da vi går fra 0, kan vi bare beregne integralet ved 1?

−p> – cos (1) = -0.540…

hvad? Er det negativt? Men det ser positivt ud i grafen.

godt … vi begik en fejl!

fordi vi skal trække integralet ved 0. Vi bør ikke antage, at det er nul.

så lad os gøre det ordentligt, trække den ene fra den anden:

1

0

1

0

=−cos(1) − (−cos (0))

= -0.540… – (-1)

= 0, 460…

det er bedre!

men vi kan have negative regioner, når kurven er under aksen:

eksempel:

det bestemte Integral, fra 1 til 3, af cos(s) d:

1

cos(s) d

Bemærk, at noget af det er positivt, og nogle negative.
den bestemte integral vil udarbejde nettoværdien.

lad os lave beregningerne:

3

1

3

1

=sin(3) − sin(1)

=0.141… − 0.841…

= -0.700…

Jump der er mere negativt end positivt med nettoresultatet på -0.700….

så vi har denne vigtige ting at huske:

b

a

f(område over aksen) − (område under aksen)

prøv at integrere cos (h) med forskellige start-og slutværdier for selv at se, hvordan positive og negative fungerer.

positivt område

men nogle gange ønsker vi, at alt område behandles som positivt (uden at delen under aksen trækkes fra).

i så fald skal vi beregne områderne separat, som i dette eksempel:

eksempel: Hvad er det samlede areal mellem y = cos(h) og H-aksen, fra H = 1 til H = 3?

dette er som det eksempel, vi lige gjorde, men nu forventer vi, at alt område er positivt (forestil dig, at vi var nødt til at male det).

så nu er vi nødt til at gøre delene separat:

• en for området over h-aksen
• en for området under h-aksen

kurven krydser h-aksen ved H = L/2, så vi har:

fra 1 til L/2:

krit/2

krit

1

cos(h) div

= sin(krit/2) − Sin(1)

= 1 − 0.841…

= 0, 159…

fra Kris/2 til 3:

div > =0,141… – 1

= -0, 859…

den sidste kommer ud negativ, men vi vil have det positivt, så:

samlet areal = 0.159… + 0.859… = 1.018…

Dette er meget forskelligt fra svaret i det foregående eksempel.

kontinuerlig

Åh ja, den funktion, vi integrerer, skal være kontinuerlig mellem a og b: ingen huller, spring eller lodrette asymptoter (hvor funktionen går op / ned mod uendelig).

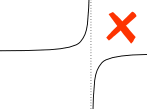
eksempel:

en lodret asymptote mellem A og b påvirker det bestemte integral.

egenskaber

område over-område under

integralet tilføjer området over aksen, men trækker området nedenfor for en “nettoværdi”:

a

integralet af G:

b

a

f(H) + g(H) D =

b

/div>

a

reversering af intervallet

reversering af retningen af intervallet giver den negative af den oprindelige retning.