De smukkeste og vigtigste matematiske ligninger
matematik er mere et maraton end en sprint — det er en lang, langsom og stabil slibning med sjældne øjeblikke af gennembrud. Alligevel får vi en gang imellem de værdsatte” Eureka ” øjeblikke, de korte linjer med bogstaver og tal, der ændrer videnskaben for evigt. Her er nogle af de mest berømte ligninger, fra de gamle grækere til moderne fysik.
Pythagoras sætning (530 f. kr.)
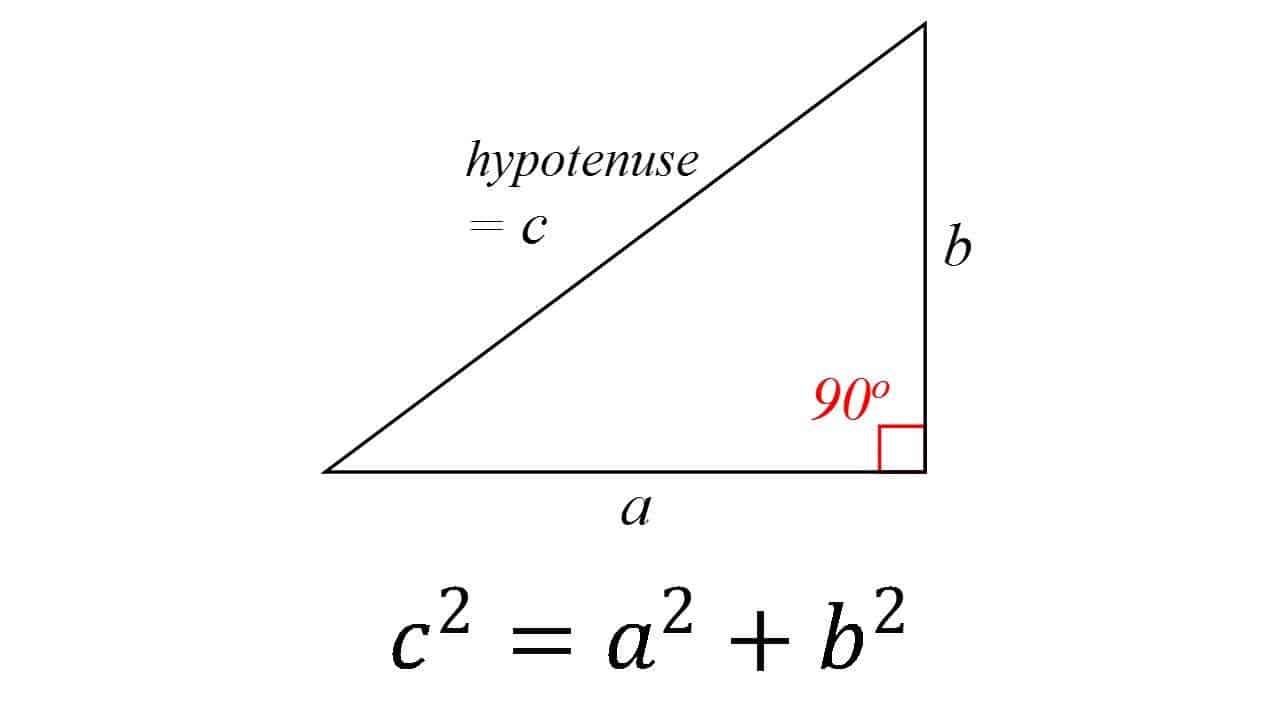
Dette er temmelig en af de grundlæggende søjler al geometri: i en højre trekant er kvadratet af hypotenusen (siden modsat den rigtige vinkel) lig med summen af kvadraterne af de to andre. Teorien tilskrives generelt den græske matematiker Pythagoras, selvom der er nogle beviser for, at babyloniske matematikere forstod formlen. Det er også meget muligt, at sætningen var kendt af mange mennesker, men han var den første til at bevise det.
sætningen har fået adskillige beviser — muligvis mest for enhver matematisk sætning. De er meget forskellige, herunder både geometriske beviser og algebraiske beviser, med nogle dating tusinder af år tilbage.
komplekse tal

den italienske matematiker Gerolamo Cardano er den første, der vides at have introduceret komplekse tal og kalder dem “fiktive” på det tidspunkt. Imidlertid tilskrives den matematiske udvikling af “jeg” som det imaginære tal, der repræsenterer kvadratroden af -1, Leonhard Euler, en af de vigtigste matematikere og forskere i menneskets historie.
komplekse tal er dybest set tal, der ikke rigtig eksisterer, men som er meget nyttige til en række beregninger. De består af tal med en reel del (de tal, vi alle kender) og en imaginær del (jeg repræsenterede her) og har praktiske anvendelser inden for mange områder, herunder fysik, kemi, biologi, økonomi, elektroteknik og statistik.
logaritmerne

logaritmer er dybest set den inverse funktion af eksponentiering. Det kan virke som kun en anden måde at skrive det samme på (og på en måde er det), men logaritmer har et utal af praktiske anvendelser, der bruges i psykologi, økonomi og målinger af mange fysiske fænomener (såsom pH eller jordskælvsstørrelse).logaritmer blev offentligt fremsat af John Napier i 1614 i en bog med titlen Mirifici Logarithmorum Canonis Descriptio (beskrivelse af den vidunderlige regel om logaritmer) — en passende titel. Et specielt tilfælde af logaritme er den naturlige logaritme-e, hvor e er et irrationelt og transcendentalt tal omtrent lig med 2.71828182845. Faktisk har e selv en fascinerende historie og et imponerende antal applikationer, men det er en historie for en anden gang.
Calculus
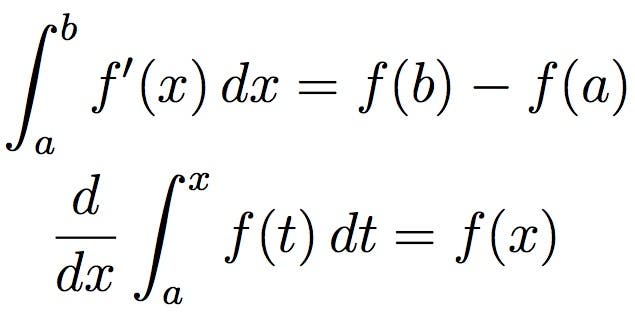
få felter i matematik har været lige så effektive som calculus. Calculus blev udviklet i det 17.århundrede af Isaac og Gottfried, og er meget udbredt inden for videnskab, teknik og økonomi. Calculus fokuserer normalt på at håndtere små mængder, især uendeligt små mængder. Gennem beregning kan disse behandles som reelle tal, selvom de teknisk set er uendeligt små.
for en enklere visualisering kan integration, afbildet ovenfor, betragtes som måling af området under en kurve, defineret af en funktion.
tyngdeloven
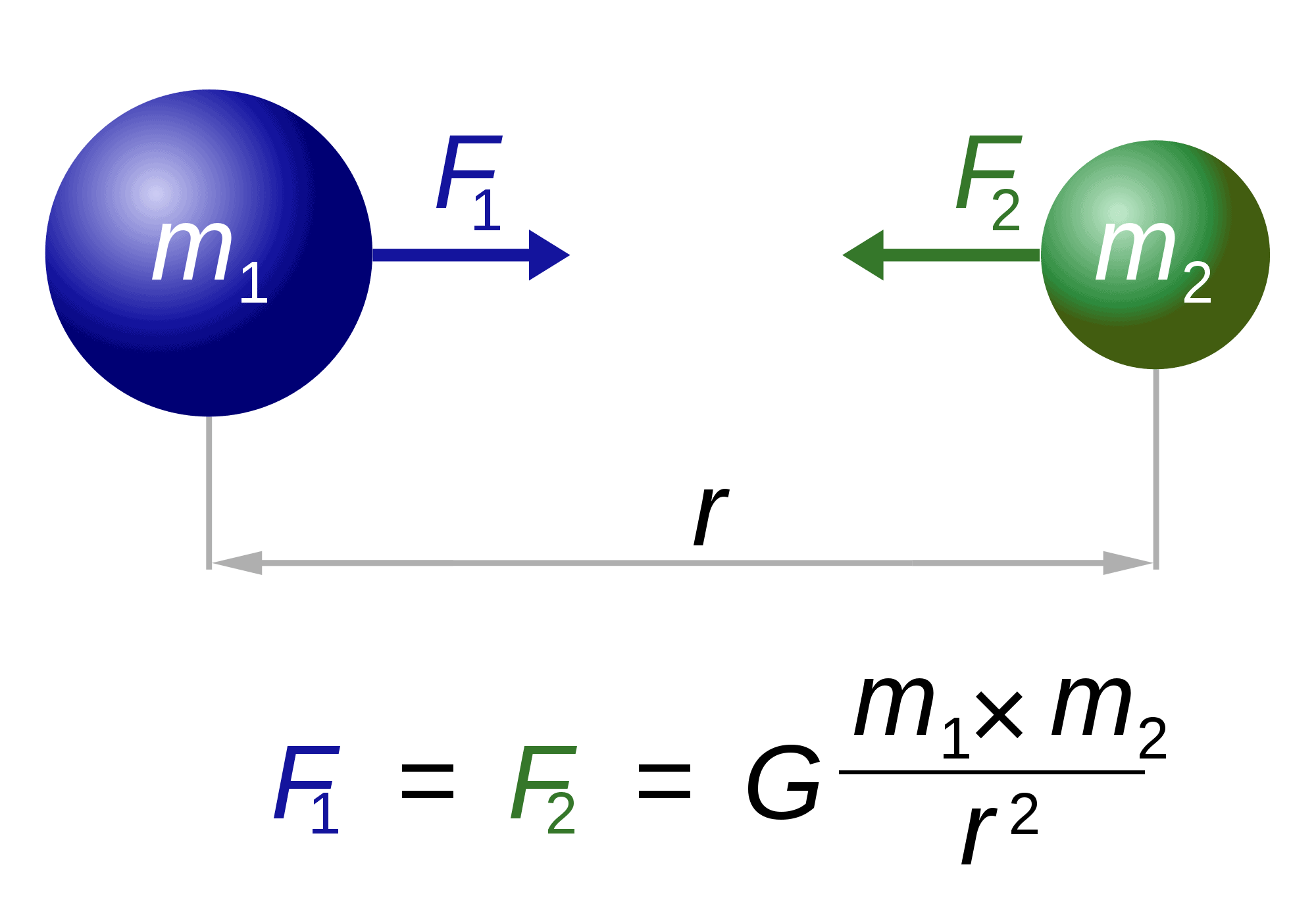
når han taler om Nyton, er han også “ansvarlig” for en af verdens mest berømte og spektakulære ligninger: tyngdeloven.
loven beskriver grundlæggende, hvordan to legemer af masserne m1 og m2 tiltrækkes af hinanden. Kraften (F1, F2) er omvendt proportional med kvadratet af afstanden mellem dem (r). Den eneste tilbageværende faktor, G, er en gravitationskonstant. Naturen af denne konstant forbliver undvigende.
generel relativitet

i næsten 200 år definerede Nytons lov vores niveau for forståelse af mekanik. Einsteins arbejde i det 20.århundrede tog tingene til det næste niveau — disse to præstationer tårner på de højeste piedestaler i fysikens verden.generel relativitet er i det væsentlige en geometrisk gravitationsteori, der generaliserer den teori, der giver en samlet beskrivelse af tyngdekraften som en geometrisk egenskab af rum og tid — eller rumtid. Især viste Einstein ikke kun, at der er sådan en ting som “rumtid”, der fusionerer de tre dimensioner med den 4.dimension af tiden, men han viste også, at denne rumtid kan bøjes af tyngdekraften, idet krumningen er direkte relateret til energien og fremdriften i uanset stof og stråling er til stede.
anden lov om termodynamik
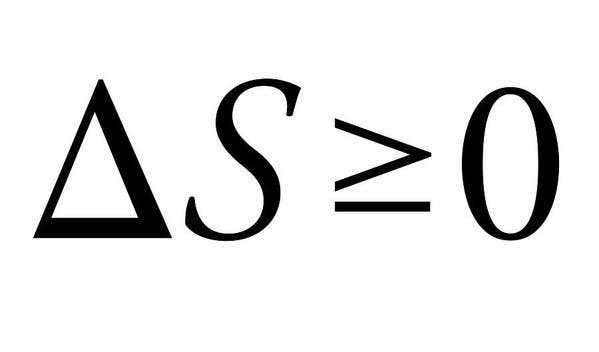
termodynamikens anden lov er, hvorfor vi ikke kan have gode ting i universet. Vittigheder til side definerer de fire love om termodynamik grundlæggende fysiske størrelser (temperatur, energi og entropi), der karakteriserer termodynamiske systemer. Især den anden skiller sig ud her på grund af sin enkelhed, men absolut massive implikationer.
loven siger i det væsentlige, at summen af entropierne i de interagerende termodynamiske systemer altid skal stige eller højst forblive konstant. Når energi skifter fra en form til en anden, eller stof bevæger sig rundt, øges entropien (eller forstyrrelsen) i et lukket system. Alle forskelle i temperatur, tryk og densitet har tendens til at flade ud efter et stykke tid
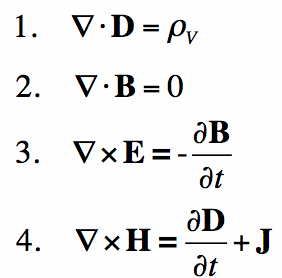
simpelthen sagt, Maksels ligninger er til elektromagnetisme, hvad Nytons lov er for mekanik. De giver et matematisk fundament for klassisk elektromagnetisme, klassisk optik og elektriske kredsløb. De er meget udbredt i selve enheden, du læser dette på-dybest set, alle elektroniske enheder.loven beskriver, hvordan elektriske og magnetiske felter genereres af ladninger, strømme og ændringer af felterne. Et betydeligt gennembrud var demonstrationen om, at elektriske og magnetiske felter formerer sig ved lysets hastighed.
Eulers identitet

endelig er dette muligvis den mest elegante ligning, en ting af højeste skønhed, fordi den involverer alle de “grundlæggende” tal:
- 0, som er neutral for addition og subtraktion;
- 1, som er neutral for multiplikation og division;
- e, hvilket er Eulers nummer (Se ovenfor), basen af naturlige logaritmer;
- jeg er den imaginære enhed (se ovenfor); og
- liter er pi, forholdet mellem omkredsen af en cirkel og dens diameter.
at finde en relation, der forener alle disse tal, er intet mindre end betagende og synes ganske usandsynligt. Demonstrationen er ikke ligefrem enkel, men du kan se den her.
det er kun passende, at Stanford University matematikprofessor Keith Devlin beskrev ligningen og sagde, at”som en Shakespeare — sonet, der fanger selve essensen af kærlighed, eller et maleri, der fremhæver skønheden i den menneskelige form, der er langt mere end bare hud dyb, Eulers ligning når ned i selve eksistensdybden”
det er ikke ofte, at matematik og fysik koges ned til enkle og elegante ligninger-men når de gør det, er det noget af et syn at se.
Leave a Reply