Articles

Cohens Kappa

by admin

evaluering af Cohens Kappa

værdien for kappa kan være mindre end 0 (negativ). En score på 0 betyder, at der er tilfældig aftale mellem raters, mens en score på 1 betyder, at der er en fuldstændig aftale mellem raters. Derfor betyder en score, der er mindre end 0, at der er mindre enighed end tilfældig chance. Nedenfor vil jeg vise dig formlen til at finde ud af dette, men det er vigtigt, at du gør dig bekendt med figur 4 for at have en stærk forståelse.

figur 4: N til at fortolke resultaterne af ratere

grunden til, at jeg fremhævede to gitter, bliver klar på et øjeblik, men lad mig nu nedbryde hvert gitter.

A = > det samlede antal forekomster, som begge ratere sagde var korrekte. Raterne er enige.

B = > det samlede antal forekomster, som Rater 2 sagde var forkert, men Rater 1 sagde var korrekte. Dette er en uenighed.

C = > det samlede antal forekomster, som Rater 1 sagde var forkert, men Rater 2 sagde var korrekte. Dette er også en uenighed.

D = > det samlede antal forekomster, som begge ratere sagde var forkerte. Ratere er enige.

for at udarbejde kappa-værdien skal vi først kende sandsynligheden for aftale (dette forklarer, hvorfor jeg fremhævede aftalens diagonale). Denne formel er afledt ved at tilføje antallet af tests, hvor raters enige derefter dividere det med det samlede antal tests. Ved hjælp af eksemplet fra figur 4 ville det betyde (A + D)/(A + B+ C+ D).

figur 5: Sandsynlighed for aftale

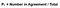
perfekt! Det næste skridt er at finde ud af sandsynligheden for tilfældig aftale. Brug af figur 4 som vejledning, den forventede værdi er det samlede antal gange, som Rater 1 sagde korrekt divideret med det samlede antal forekomster, ganget med det samlede antal gange, som Rater 2 sagde korrekt divideret med det samlede antal forekomster, føjet til det samlede antal gange, som Rater 1 sagde forkert ganget med det samlede antal gange, som Rater 2 sagde forkert. Det er en masse information at tage derind, så i figur 6 har jeg formuleret denne ligning ved hjælp af gitteret ovenfor.

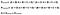
Figure 6: Formula to derive probability of random agreement

Lastly, the formula for Cohen’s Kappa is the probability of agreement take away the probability of random agreement divided by 1 minus the probability of random agreement.

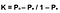
Figure 7: Cohens Kappa koefficient formel.

fantastisk! Du er nu i stand til at skelne mellem pålidelighed og gyldighed, forklare Cohens kappa og evaluere det. Denne statistik er meget nyttig, selvom jeg har forstået, hvordan det virker, tror jeg nu, at det kan være underudnyttet, når man optimerer algoritmer til en bestemt metrisk. Derudover gør Cohens kappa også et godt stykke arbejde med at måle både multi-klasse og ubalancerede klasseproblemer.

P. S. Hvis der er noget, du vil have mig til at dække at gøre med datavidenskab, kan du sende en besked til mig på kvidre @KurtisPykes eller efterlade et svar på dette indlæg.