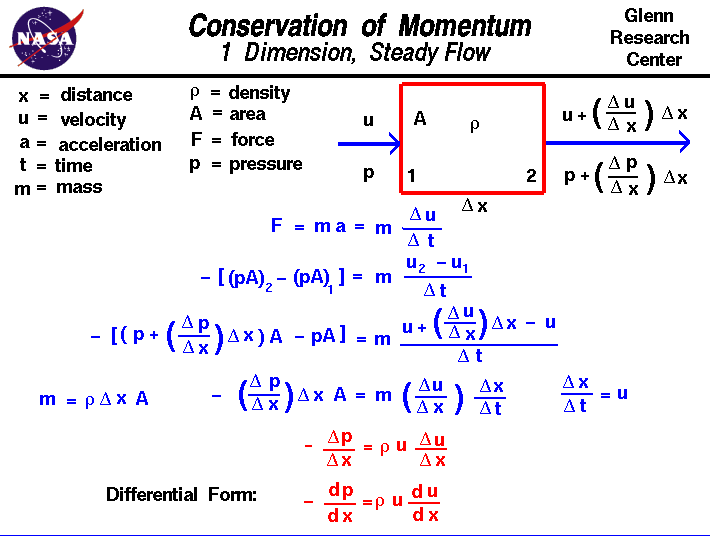
bevarelsen af momentum er et grundlæggende koncept for fysiksammen medbevarelse af energiogbevarelse af masse.Momentum er defineret som massen af et objekt multipliceret med hastighedenaf objektet.Bevarelsen af momentum siger, at inden for et problemdomæne forbliver mængden af momentum konstant;momentum er hverken skabt eller ødelagt, men kun ændretgennem styrkernes handling som beskrevet af bevægelse.At håndtere momentum er vanskeligere end at håndtere masse og energi, fordiøjeblikket er avektormængde med både en størrelse og en retning. Momentum er bevaret i alle trefysiske retninger på samme tid. Det er endnu vanskeligere, når man beskæftiger sig med agasfordi kræfter i en retning kan påvirke momentum i en anden retningpå grund af kollisioner af mange molekyler.På dette dias vil vi præsentere et meget, meget forenklet strømningsproblem, hvor egenskaber kun ændres i en retning.Problemet forenkles yderligere ved at overveje en stabil strømning, som ikke ændrer sig med tiden, og ved at begrænse kræfterne til kun dem, der er forbundet med thepressure.Be klar over, at reelle strømningsproblemer er meget mere komplekseend dette enkle eksempel.

lad os overveje strømmen af en gas gennem et domæne, hvor strømningsegenskaberkun ændre sig i en retning, som vi vil kalde “h”. Gassen kommer ind i domainat station 1 med en vis hastighed u og noget tryk pand går ud på station 2 med en anden værdi af hastighed og tryk. For enkelhed antager vi detdensiteten r forbliver konstant inden for domænetog at det område A, gennem hvilket gasstrømme også forbliver konstant. Placeringen af stationer 1 og 2 er adskilletaf en afstand kaldet del h. (Delta er den lille trekant på glideog er det græske bogstav “d”. Matematikere bruger ofte dette symbol til at betegneen ændring eller variation af en mængde. Skrifttypen på internettet understøtter ikkede græske bogstaver, så vi vil bare kalde det “del”.) En ændring med afstand kaldes en gradientfor at undgå forvirring med en ændring med tiden, der kaldes en sats.Hastighedsgradienten er angivet med del u / del; ændringen i hastighedsændring i afstand. Så på station 2 er hastigheden givet af hastighedenat 1 plus gradienten gange afstanden.

et lignende udtryk giver trykketved udgangen:

nyDen anden bevægelseslov angiver, at kraft F er lig med ændringen i momentum medrespekt for tiden. For et objekt med konstant massm reduceres dette til massetidernes acceleration a.An acceleration er en ændring i hastighed med en ændring i tid(Del u / del t). Derefter:

kraften i dette problemkommer fra trykgradienten. Arealenhed, er nettokraften på vores væskedomæne trykket gange området vedudgang minus trykket gange området ved indgangen.

minustegnet påbegyndelsen af dette udtryk bruges, fordi gasser bevæger sig fra et område med højt tryk til et område med lavt tryk; hvis trykket stiger med en gang, vil hastigheden falde. Udskiftning af vores udtryk for hastighedog tryk:

forenkle:

bemærker, at (del H / Del t) er thevelocity, og at massen er densiteten r gange volumen (område gange del h):

forenkle:

del p / del h og del u / del h repræsenterer tryk-og hastighedsgradienterne.Hvis vi krymper vores domæne ned til forskellige størrelser, bliver disse gradienter forskelle:

Dette er en endimensionel, stabil form ofeulers Equation.It er interessant at bemærke, at trykfaldaf en væske (udtrykket til venstre) er proportional med både værdien afvelocity og gradienten af hastigheden.En løsning af denne momentumligning giver os form afdynamisk trykder vises ibernoullis ligning.

aktiviteter:
guidede ture

• grundlæggende væskedynamik ligninger:

Navigation ..

Begyndervejledning Startside