Beans magasin
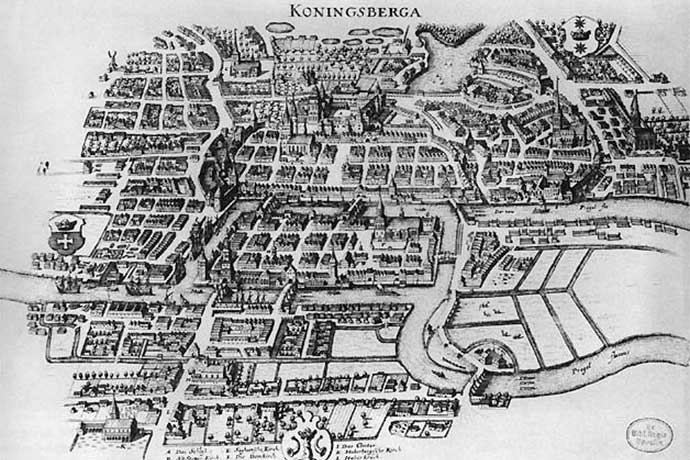
kort af Merian-Erben (1652) på
denne måneds matematikpuslespil går tilbage til 1735, da det først blev løst af Leonhard Euler, en svensk matematiker og fysiker.
puslespillet hedder de syv broer i K. K. Det er baseret på en egentlig by, derefter i Preussen, nu Kaliningrad i Rusland. Byen er delt af en flod med to øer imellem og, længere nedstrøms, floden deler byen igen.
problemet er bedragerisk simpelt: der er (eller var på Eulers tid) syv broer til at forbinde de to øer og de nedstrøms dele af byen. Euler spekulerede på, om en person kunne gå over hver af de syv broer en gang og kun en gang for at røre ved alle dele af byen. Start og Slut på samme sted var ikke et krav.
Her er et kort, du kan bruge til at forsøge at løse problemet for dig selv:
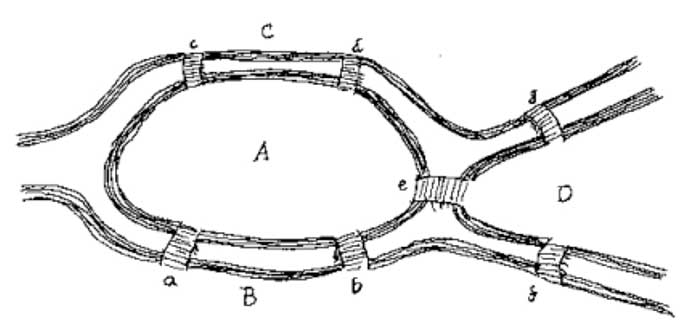
som tror du er mere vigtigt at løse dette problem: antallet af broer eller placeringen af hver bro?
svar: antallet af broer.
Euler beviste, at antallet af broer skal være et lige antal, for eksempel seks broer i stedet for syv, hvis du vil gå over hver bro en gang og rejse til hver del af K Kurstnigsberg. Løsningen ser hver bro som et endepunkt, et toppunkt i matematiske termer og forbindelserne mellem hver bro (toppunkt). Euler indså, at kun et lige antal broer gav det rigtige resultat af at kunne røre ved alle dele af byen uden at krydse en bro to gange.
Euler brugte matematik til at bevise, at det var umuligt at krydse alle syv broer kun en gang og besøge alle dele af K. Dermed satte han i gang en række opdagelser og indsigter om, hvordan rum og krydsende rum kan defineres, såvel som deres egenskaber. En detaljeret beskrivelse af Eulers løsning i linket under denne artikel.
Hvis du nogensinde har set en mobius-strimmel, har du for eksempel set et eksempel på topologi, et matematisk fagområde udviklet sig fra Eulers løsning på dette problem. Topologi beskæftiger sig med rum og hvordan ting forbinder hinanden, såvel som kontinuitet og grænser for rummet. Topologi studerer også, hvordan egenskaber ved et rum ændres og ikke ændres, når rummet udvides eller kontraheres.
i computing er topologi nyttig til at forstå netværk (stier) data kan strømme inden for ethvert system, samt hvordan datasæt kan relateres til hinanden. De syv broer i K. K. Kristnigsberg ligner også et andet almindeligt computerproblem, der undertiden kaldes Traveling Salesman-problemet, hvor du prøver at finde den mest effektive rute givet et sæt begrænsninger som de syv broer i Eulers problem.
ikke-matematikere (sandsynligvis dig, bestemt mig) oplever det rejsende Sælgerproblem, når vi kommer på et tog eller en bus. Problemet med rejsende sælger er at finde ud af den mest effektive måde at rejse mellem par af byer med bestemte afstande. Håndtering af knappe ressourcer (tog, busser), der kører langs endelige ruter, er et perfekt problem for computing at løse, fordi computere er hurtigere og mere effektive. Men først har vi brug for Euler og andre til at angive problemet og definere løsninger med matematik. Vi programmerer derefter vores computere til at lave matematikken.
topologi beskæftiger sig også med sætteori, hvordan grupper af ting kan sorteres i sæt for at identificere fælles elementer med andre grupper såvel som unikke elementer. Et Venn-diagram er et godt eksempel på et sæt. Og programmering skal undertiden sortere data på forskellige måder. Hvilken sorteringsmetode der fungerer bedst for en situation kan bestemmes ved sætteori.
og hvad skete der med de syv broer fra Eulers tid? To overlevede ikke anden verdenskrig. to broer blev revet ned og erstattet med en enkelt motorvej. Af de tre resterende broer blev den ene genopbygget i 1935, mens de to andre forbliver intakte, da Euler kendte dem. Og selvfølgelig har K. K., Preussen, skiftet navn til Kaliningrad, Rusland.
Leave a Reply