9.4: ionbinding
Energetik ved dannelse af ionbinding
ionbindinger dannes, når positivt og negativt ladede ioner holdes sammen af elektrostatiske kræfter. Overvej et enkelt par ioner, en kation og en anion. Hvor stærk vil kraften i deres tiltrækning være? I henhold til Coulombs lov er energien fra den elektrostatiske tiltrækning (\(E\)) mellem to ladede partikler proportional med størrelsen af ladningerne og omvendt proportional med den internukleære afstand mellem partiklerne (\(r\)):
\
\
hvor hver ions ladning er repræsenteret af symbolet K. proportionalitetskonstanten k er lig med 2,31 liter 10-28 J·m. denne værdi af k inkluderer ladningen af en enkelt elektron (1,6022 liter 10-19 C) for hver ion. Ligningen kan også skrives ved hjælp af ladningen af hver ion, udtrykt i coulombs (C), inkorporeret i konstanten. I dette tilfælde er proportionalitetskonstanten, k, lig med 8.999 liter 109 J·m/C2. I det givne eksempel er 1.kvartal = +1(1,6022-10-19 C) og 2. kvartal = -1(1,6022-10-19 C). Hvis 1.kvartal og 2. kvartal har modsatte tegn (som i NaCl, for eksempel hvor 1. kvartal er +1 For Na+ og 2. kvartal er -1 for Cl−), så er e negativ, hvilket betyder, at energi frigives, når modsat ladede ioner bringes sammen fra en uendelig afstand for at danne et isoleret ionpar.
energi frigives altid, når der dannes en binding, og tilsvarende kræver det altid energi for at bryde en binding.
som vist ved den grønne kurve i den nederste halvdel af figuren \(\Sideindeks{1}\), vil den maksimale energi blive frigivet, når ionerne er uendeligt tæt på hinanden ved r = 0. Fordi ioner optager plads og har en struktur, hvor den positive kerne er omgivet af elektroner, kan de imidlertid ikke være uendeligt tæt på hinanden. På meget korte afstande bliver frastødende elektron-elektroninteraktioner mellem elektroner på tilstødende ioner stærkere end de attraktive interaktioner mellem ioner med modsatte ladninger, som vist ved den røde kurve i den øverste halvdel af figuren \(\Sideindeks{1}\). Systemets samlede energi er en balance mellem de attraktive og frastødende interaktioner. Den lilla kurve i figur \(\Sideindeks{1}\) viser, at systemets samlede energi når et minimum ved r0, det punkt, hvor de elektrostatiske afstødninger og attraktioner er nøjagtigt afbalancerede. Denne afstand er den samme som den eksperimentelt målte bindingsafstand.
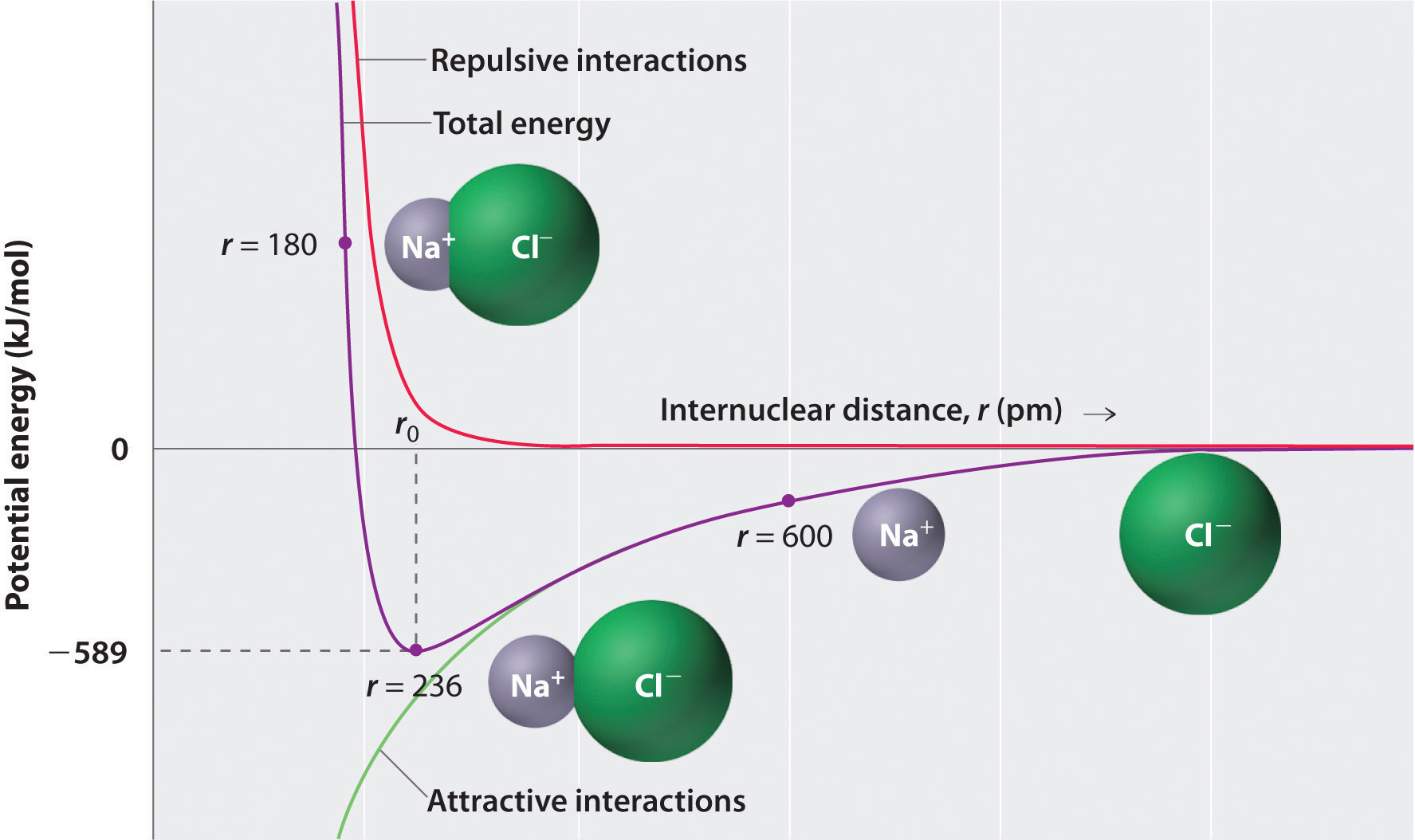
Overvej den energi, der frigives, når en gasformig \(Na^+\) ion og en gasformig \(Cl^-\) ion bringes sammen fra r = liter til r = r0. I betragtning af at den observerede gasfase internukleære afstand er 236 pm, er energiændringen forbundet med dannelsen af et ionpar fra en \(Na^+_{(g)}\) ion og en \(Cl^-_{(g)}\) ion som følger:
\ &= (2,31 \gange {10^ {- 28}}\rm{J}\cdot \Annuller{m} ) \left( \dfrac{( + 1)( – 1)}{236\; \Annuller{pm} \ gange 10^ {- 12} \Annuller{m/pm}} \højre) \\ &= – 9.79 \ gange 10^ {- 19}\; J/ion\; par \label{EK2} \end{align*}\]
den negative værdi indikerer, at energi frigives. Vores konvention er, at hvis en kemisk proces giver energi til omverdenen, er energiændringen negativ. Hvis det kræver energi, er energiændringen positiv. For at beregne energiændringen i dannelsen af en mol NaCl-par, er vi nødt til at multiplicere energien pr. ionpar med Avogadros nummer:
\
dette er den energi, der frigives, når der dannes 1 mol gasformige ionpar, ikke når 1 mol positive og negative ioner kondenserer for at danne et krystallinsk gitter. På grund af langtrækkende interaktioner i gitterstrukturen svarer denne energi ikke direkte til gitterenergien i det krystallinske faste stof. Den store negative værdi indikerer imidlertid, at det at bringe positive og negative ioner sammen er energisk meget gunstigt, uanset om der dannes et ionpar eller et krystallinsk gitter.
vi opsummerer de vigtige punkter om ionbinding:
- ved r0 er ionerne mere stabile (Har en lavere potentiel energi) end de er i en uendelig internuklear afstand. Når modsat ladede ioner bringes sammen fra r = liter til r = r0, sænkes systemets energi (energi frigives).
- på grund af den lave potentielle energi ved r0 skal der tilføjes energi til systemet for at adskille ionerne. Den nødvendige mængde energi er bindingsenergien.
- systemets energi når et minimum ved en bestemt internuklear afstand (bindingsafstanden).
eksempel \(\Sideindeks{2}\): Lif
Beregn mængden af energi, der frigives, når 1 mol gasformige Li+F− ionpar dannes fra de adskilte ioner. Den observerede internukleære Afstand i gasfasen er 156 pm.
givet: kation og anion, mængde og internuklear afstand
bedt om: energi frigivet fra dannelse af gasformige ionpar
strategi:
erstat de relevante værdier i ligning \(\ref{Ek1b}\) for at opnå den energi, der frigives i dannelsen af et enkelt ionpar, og multiplicer derefter denne værdi med Avogadros nummer for at opnå den frigjorte energi pr.mol.
opløsning:
indsættelse af værdierne for Li+F− i ligning \(\ref{Ek1b}\) (hvor 1. kvartal = +1, 2. kvartal = -1 og r = 156 pm) finder vi, at den energi, der er forbundet med dannelsen af et enkelt par Li+F− ioner, er
\ &=\left(2,31 \gange 10^{-28} j}\højre) \venstre (\dfrac {\tekst{(+1)(-1)}}{156\; pm \times 10^{-12} \ Annuller{m / pm}} \ right)\ \ & =-1.48 \ times 10^{-18} \ end{align*}\]
så er energien frigivet pr. mol Li+F− ionpar
\ &-891 \;kJ / mol \ end{align*}\]
fordi Li+ og F− er mindre end Na+ og Cl− (se afsnit 7.3), er den internukleære Afstand i LiF kortere end i NaCl. Følgelig frigives der i overensstemmelse med ligning \(\ref{Ek1b}\) meget mere energi, når der dannes 1 mol gasformige Li+F− ionpar (-891 kJ/mol) end når der dannes 1 mol gasformige Na+Cl− ionpar (-589 kJ/mol).
øvelse \(\Sideindeks{2}\): Magnesiumfilter
Beregn mængden af energi, der frigives, når 1 mol gasformige \(\ce{MgO}\) ionpar dannes fra de adskilte ioner. Den internukleære Afstand i gasfasen er 175 pm.
svar
-3180 kJ / mol = -3.18 ret 103 kJ / mol
Leave a Reply