forståelse af ækvivalente fraktioner

ækvivalente fraktioner repræsenterer den samme del af en helhed

den bedste måde at tænke på ækvivalente fraktioner er, at de er fraktioner, der har den samme samlede værdi.

for eksempel, hvis vi skærer en tærte nøjagtigt ned i midten, i to lige store stykker, er et stykke det samme som den ene halvdel af kagen.

og hvis en anden tærte (samme størrelse) skæres i 4 lige store stykker, repræsenterer to stykker af den tærte den samme mængde tærte, som 1/2 gjorde.

så vi kan sige, at 1/2 er ækvivalent (eller lig) til 2/4.

lad ikke tilsvarende fraktioner forvirre dig!

Tag et kig på de fire cirkler ovenfor.Kan du se, at den ene “1/2”, de to “1/4” og de fire “1/8” optager den samme mængde område farvet i orange for deres cirkel?Nå det betyder, at hvert område farvet i orange er en tilsvarende brøkdel eller lige stor mængde. Derfor kan vi sige, at 1/2 er lig med 2/4, og 1/2 er også lig med 4/8. Og ja grasshopper, 2/4 er en ækvivalent fraktion for 4/8 too.As du ved allerede, vi er nødder om regler. Så lad os se på reglen for at kontrollere, om to fraktioner er ækvivalente eller ens. Reglen for ækvivalente fraktioner kan være lidt svært at forklare, men hænge derinde, vi vil rydde op i bare en smule.

Her er reglen

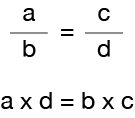
hvad denne regel siger er, at to fraktioner kun er ækvivalente (lige), hvis produktet af tælleren (A) af den første fraktion og nævneren (d) af den anden fraktion er ens til produktet af nævneren (B) af den første fraktion og tælleren (C) af den anden fraktion.

et produkt betyder simpelthen, at du multiplicerer.

det lyder som en mundfuld, så lad os prøve det med tal …

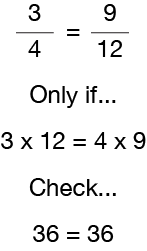
Test reglen

lad os nu sætte tallene i reglen for ækvivalente fraktioner for at være sikker på at du har det nede “koldt”. 3/4 er kun ækvivalent (lig) med 9/12, hvis produktet af tælleren (3) i den første fraktion og nævneren (12) i den anden fraktion er lig med produktet af nævneren (4) i den første fraktion og tælleren (9) i den anden fraktion. Så vi ved, at 3/4 svarer til 9/12, fordi 3 liter 12=36 og 4 liter 9=36. En enkel måde at se på, hvordan man kontrollerer for ækvivalente fraktioner, er at gøre det, der kaldes “cross-multiplicer”, hvilket betyder multiple tælleren for en brøkdel med nævneren for den anden fraktion. Så gør det samme omvendt. Sammenlign nu de to svar for at se, om de er ens. Hvis de er ens, er de to fraktioner ækvivalente fraktioner.

grafikken nedenfor viser dig, hvordan du krydser multiplicer…

Okay, lad os gøre et med tal, hvor fraktionerne ikke er ækvivalente…

som du kan se ved dette eksempel, er 1/2 ikke en ækvivalent brøkdel af 2/3.

Hvis du husker at bruge cross-multiplicer-metoden, skal du ikke have nogen problemer med at verificere ækvivalente fraktioner.

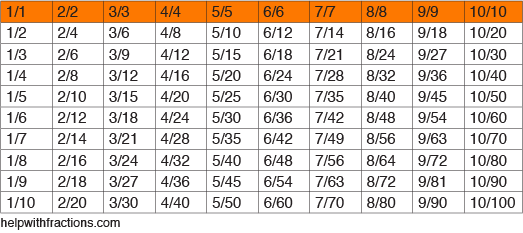
nedenstående tabel viser nogle almindelige fraktioner og deres ækvivalenter. Bare læs bordet fra venstre mod højre. Hvad det viser dig er værdier ganget med forskellige variationer af fraktioner svarende til “1”. Du kan huske, at ethvert tal divideret med sig selv er lig med “1” ret?