AUC-ROC kurva – stjärnan Artist!

Du har byggt din maskininlärningsmodell – så vad är nästa? Du måste utvärdera det och validera hur bra (eller dåligt) det är, så du kan sedan bestämma om du ska implementera det. Det är där AUC-ROC-kurvan kommer in.

namnet kan vara en munfull, men det säger bara att vi beräknar ”området under kurvan” (AUC) för ”Receiver Characteristic Operator” (ROC). Förvirrad? Jag känner dig! Jag har varit i dina skor. Men oroa dig inte, vi kommer att se vad dessa termer betyder i detalj och allt kommer att bli en bit tårta!

För nu vet bara att AUC-ROC-kurvan hjälper oss att visualisera hur bra vår maskininlärningsklassificerare utför. Även om det bara fungerar för binära klassificeringsproblem, kommer vi att se mot slutet hur vi kan utöka det för att utvärdera klassificeringsproblem i flera klasser också.

Vi kommer också att täcka ämnen som känslighet och specificitet eftersom dessa är viktiga ämnen bakom AUC-ROC-kurvan.

Jag föreslår att du går igenom artikeln om Förvirringsmatris eftersom det kommer att introducera några viktiga termer som vi kommer att använda i den här artikeln.

Innehållsförteckning

• Vad är känslighet och specificitet?
• Sannolikhet för förutsägelser
• vad är AUC-ROC-kurvan?
• hur fungerar AUC-ROC-kurvan?
• AUC-ROC i Python
• AUC-ROC för klassificering i flera klasser

Vad är känslighet och specificitet?

Så här ser en förvirringsmatris ut:

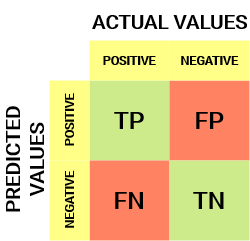
från förvirringsmatrisen kan vi härleda några viktiga mätvärden som inte diskuterades i föregående artikel. Låt oss prata om dem här.

känslighet / sann positiv hastighet / återkallelse

känslighet berättar vilken andel av den positiva klassen som har klassificerats korrekt.

ett enkelt exempel skulle vara att bestämma vilken andel av de faktiska sjuka personerna som upptäcktes korrekt av modellen.

False Negative Rate

False Negative Rate (FNR) berättar vilken andel av den positiva klassen som felaktigt klassificerats av klassificeraren.

en högre TPR och en lägre FNR är önskvärd eftersom vi vill klassificera den positiva klassen korrekt.

specificitet / sann negativ hastighet

specificitet berättar vilken andel av den negativa klassen som har klassificerats korrekt.

med samma exempel som i känslighet skulle specificitet innebära att man bestämmer andelen friska människor som identifierades korrekt av modellen.

falsk positiv hastighet

FPR berättar vilken andel av den negativa klassen som felaktigt klassificerats av klassificeraren.

en högre TNR och en lägre FPR är önskvärd eftersom vi vill klassificera den negativa klassen korrekt.

av dessa mätvärden är känslighet och specificitet kanske det viktigaste och vi kommer senare att se hur dessa används för att bygga en utvärderingsmetrisk. Men innan det, låt oss förstå varför sannolikheten för förutsägelse är bättre än att förutsäga målklassen direkt.

Sannolikhet för förutsägelser

en maskininlärningsklassificeringsmodell kan användas för att förutsäga den faktiska klassen av datapunkten direkt eller förutsäga sannolikheten för att tillhöra olika klasser. Det senare ger oss mer kontroll över resultatet. Vi kan bestämma vår egen tröskel för att tolka resultatet av klassificeraren. Detta är ibland mer försiktigt än att bara bygga en helt ny modell!att ställa in olika tröskelvärden för klassificering av positiv klass för datapunkter ändrar oavsiktligt modellens känslighet och specificitet. Och en av dessa trösklar kommer förmodligen att ge ett bättre resultat än de andra, beroende på om vi syftar till att sänka antalet falska negativ eller falska positiva.

ta en titt på tabellen nedan:

mätvärdena ändras med de ändrade tröskelvärdena. Vi kan generera olika förvirringsmatriser och jämföra de olika mätvärdena som vi diskuterade i föregående avsnitt. Men det skulle inte vara en försiktig sak att göra. Istället kan vi skapa en plot mellan några av dessa mätvärden så att vi enkelt kan visualisera vilken tröskel som ger oss ett bättre resultat.

AUC-ROC-kurvan löser just det problemet!

vad är AUC-ROC-kurvan?

Roc-kurvan (Receiver Operator Characteristic) är ett utvärderingsmått för binära klassificeringsproblem. Det är en sannolikhetskurva som plottar TPR mot FPR vid olika tröskelvärden och i huvudsak separerar ’signalen’ från ’bruset’. Området Under kurvan (AUC) är måttet på förmågan hos en klassificerare att skilja mellan klasser och används som en sammanfattning av ROC-kurvan.

ju högre AUC, desto bättre prestanda för modellen när man skiljer mellan de positiva och negativa klasserna.

När AUC = 1, kan klassificeraren perfekt skilja mellan alla positiva och negativa klasspunkter korrekt. Om, dock, AUC hade varit 0, då klassificeraren skulle förutsäga alla negativa som positiva, och alla positiva som negativa.

När 0.5<AUC<1, Det finns en stor chans att klassificeraren kommer att kunna skilja de positiva klassvärdena från de negativa klassvärdena. Detta beror på att klassificeraren kan upptäcka fler antal sanna positiva och sanna negativa än falska negativa och falska positiva.

När AUC=0,5, kan klassificeraren inte skilja mellan positiva och negativa klasspunkter. Betyder antingen klassificeraren förutspår slumpmässig klass eller konstant klass för alla datapunkter.

ju högre AUC-värde för en klassificerare desto bättre är dess förmåga att skilja mellan positiva och negativa klasser.

hur fungerar AUC-ROC-kurvan?

i en ROC-kurva indikerar ett högre X-axelvärde ett högre antal falska positiva än sanna negativa. Medan ett högre Y-axelvärde indikerar ett högre antal sanna positiva än falska negativa. Så valet av tröskeln beror på förmågan att balansera mellan falska positiva och falska negativa.

låt oss gräva lite djupare och förstå hur vår ROC-kurva skulle se ut för olika tröskelvärden och hur specificiteten och känsligheten skulle variera.

Vi kan försöka förstå denna graf genom att generera en förvirringsmatris för varje punkt som motsvarar en tröskel och prata om prestanda för vår klassificerare:

punkt A är där känsligheten är den högsta och specificiteten den lägsta. Detta innebär att alla positiva klasspoäng klassificeras korrekt och alla negativa klasspoäng klassificeras felaktigt.

faktum är att varje punkt på den blå linjen motsvarar en situation där sann positiv hastighet är lika med falsk positiv hastighet.

alla punkter ovanför denna rad motsvarar situationen där andelen korrekt klassificerade punkter som tillhör den positiva klassen är större än andelen felaktigt klassificerade punkter som tillhör den negativa klassen.

Även om punkt B har samma känslighet som punkt A, har den en högre specificitet. Vilket innebär att antalet felaktigt negativa klasspoäng är lägre jämfört med föregående tröskel. Detta indikerar att denna tröskel är bättre än den föregående.

mellan punkterna C och D är känsligheten vid punkt C högre än punkt D för samma specificitet. Detta innebär, för samma antal felaktigt klassificerade negativa klasspoäng, klassificeraren förutspådde ett högre antal positiva klasspoäng. Därför är tröskeln vid punkt C bättre än punkt D.

nu, beroende på hur många felaktigt klassificerade punkter vi vill tolerera för vår klassificerare, skulle vi välja mellan punkt B eller C för att förutsäga om du kan besegra mig i PUBG eller inte.

” falska förhoppningar är farligare än rädsla.”- J. R. R. Tolkein

punkt E är där specificiteten blir högst. Det betyder att det inte finns några falska positiva klassificerade av modellen. Modellen kan korrekt klassificera alla negativa klasspoäng! Vi skulle välja denna punkt om vårt problem var att ge perfekta låtrekommendationer till våra användare.

går du med denna logik, kan du gissa var punkten som motsvarar en perfekt klassificerare skulle ligga på grafen?

Ja! Det skulle vara i det övre vänstra hörnet av ROC-grafen som motsvarar koordinaten (0, 1) i det kartesiska planet. Det är här att både känsligheten och specificiteten skulle vara den högsta och klassificeraren skulle korrekt klassificera alla positiva och negativa klasspunkter.

förstå AUC-ROC-kurvan i Python

Nu kan vi antingen manuellt testa känsligheten och specificiteten för varje tröskel eller låta sklearn göra jobbet åt oss. Vi går definitivt med det senare!

låt oss skapa våra godtyckliga data med sklearn make_classification-metoden:

Jag kommer att testa prestanda för två klassificerare på denna dataset:

Sklearn har en mycket potent metod roc_curve() som beräknar ROC för din klassificerare på några sekunder! Den returnerar FPR -, TPR-och tröskelvärdena:

AUC-poängen kan beräknas med roc_auc_score () – metoden för sklearn:

0.9761029411764707 0.9233769727403157

prova den här koden i fönstret live coding nedan:

Vi kan också plotta ROC-kurvorna för de två algoritmerna med matplotlib:

det framgår av diagrammet att AUC för den logistiska Regressionsroc-kurvan är högre än för KNN ROC-kurvan. Därför kan vi säga att logistisk regression gjorde ett bättre jobb med att klassificera den positiva klassen i datasetet.

AUC-ROC för klassificering i flera klasser

som jag sa tidigare är AUC-ROC-kurvan endast för binära klassificeringsproblem. Men vi kan utvidga det till flerklassklassificeringsproblem genom att använda One vs All-tekniken.

Så, om vi har tre klasser 0, 1 och 2, kommer ROC för klass 0 att genereras som att klassificera 0 mot Inte 0, dvs 1 och 2. ROC för klass 1 kommer att genereras som klassificering 1 Mot inte 1, och så vidare.

ROC-kurvan för klassificeringsmodeller i flera klasser kan bestämmas enligt nedan:

End Notes

Jag hoppas att du hittade den här artikeln användbar för att förstå hur kraftfull AUC-ROC-kurvmätaren är för att mäta prestanda för en klassificerare. Du kommer att använda detta mycket i branschen och även i datavetenskap eller maskininlärning hackathons. Bättre bekanta dig med det!

gå vidare Jag skulle rekommendera dig följande kurser som kommer att vara användbara för att bygga din datavetenskap:

• introduktion till datavetenskap
• tillämpad maskininlärning

du kan också läsa den här artikeln på vår mobilapp