4-fargeproblemet er et av de mest kjente matematiske problemene. Det motstod bevis i mer enn hundre år før det endelig bukket seg; til slutt var det et gyldig bevis, men en som stod på mer enn tusen timer datamaskintid. Jim Tilleys forskning tyder på at en dramatisk forenkling til slutt kan være mulig. Han har oppdaget en eiendom, Kempe-låsing, at et minimum counterexample til 4-farge teoremet må vise og har formulert en formodning, basert på omfattende undersøkelser, At Birkhoff diamant er den eneste grunnleggende kempe-låsing konfigurasjon.

graffarging innebærer å tilordne etiketter eller farger til hjørnene i et matematisk objekt kjent som en graf. 4-fargeproblemet ga en av de opprinnelige motivasjonene for utviklingen av algebraisk grafteori. Graffarging brukes i mange virkelige problemer, for eksempel å minimere konflikter når du planlegger sportsarrangementer, planlegge eksamensplaner og organisere sitteplaner, selv FOR CCTV-kameraplassering i en bygning med mange hjørner for å minimere kameraoverlapping. Det gir også grunnlaget for Sudoku-oppgaver.

4-fargeproblemet
Francis Guthrie, en student av den berømte Britiske matematikeren Og logikeren Augustus De Morgan, utgjorde 4-fargeproblemet i 1852. Han formulerte problemet med hensyn til kart som tilfredsstiller visse forhold, for eksempel ikke inneholder noen hull og har hver region (f. eks land eller stat) koblet slik at ingen region eksisterer i to eller flere ikke-sammenhengende deler. Guthrie hevdet at for slike kart ville det aldri ta mer enn fire farger for å farge kartet slik at ingen to naboregioner var samme farge.

i Dag er 4-fargeproblemet uttrykt i form av grafer, og i stedet for å fargelegge regioner i kart, farger man hjørner i grafer. Alle eksisterende bevis på 4-fargesetningen viser at et minimums moteksempel ikke kan eksistere. (Et minimum counterexample er den minste plane grafen som krever mer enn fire farger for en riktig farging av sine hjørner.) Bare plan grafer som er trianguleringer må vurderes, da en graf som ikke er en triangulering, kan omdannes til en ved å sette inn kanter. Hvis den resulterende trianguleringen er 4-colourable, er den opprinnelige grafen også 4-colourable. Det er svært nyttig å kunne begrense ens gransking til trianguleringer.

Et tidlig forsøk på bevis
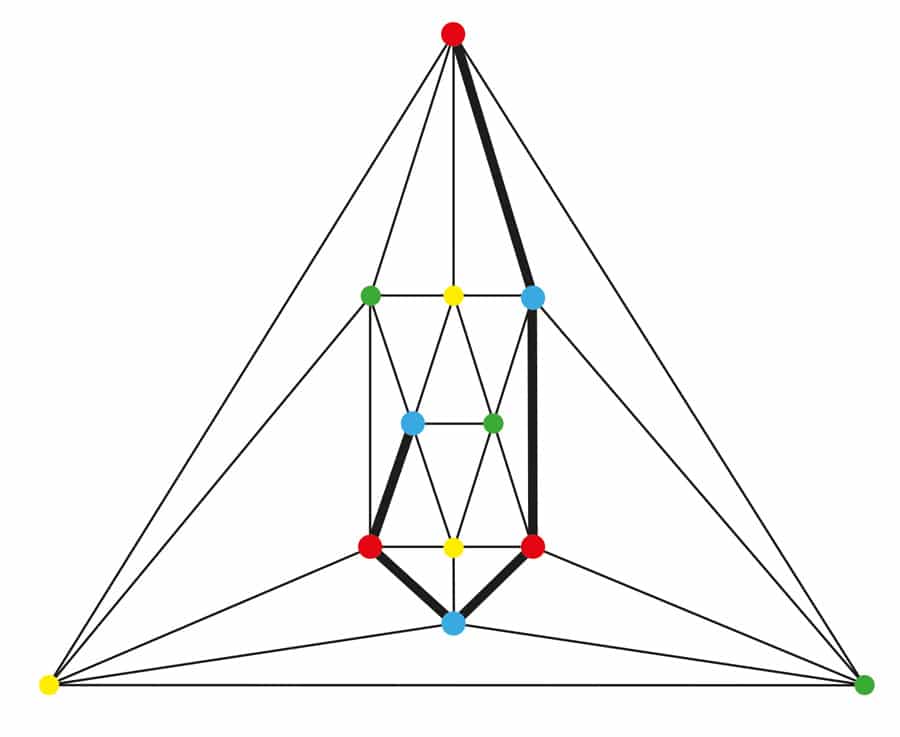
av de som tilbød et bevis, Alfred Bray Kempe, en engelsk advokat og amatørmatematiker, var den personen hvis rykte var mest besmittet av hans mislykkede innsats. Han annonserte sin suksess i 1879 og hans’ bevis ‘ ble publisert I American Journal Of Mathematics. Elleve år senere skapte En annen engelsk matematiker, Percy Heawood, et kart som han 4-farget opp til den endelige regionen på en slik måte at Kempes metode mislyktes for den endelige regionen. Til tross for hans fiasko forlot Kempe et nyttig verktøy-En kempe-kjede. Det er en maksimal, tilkoblet (hvert toppunkt kan nås fra noen andre ved en sti langs kanter) subgraph der alle hjørner bruker nøyaktig to farger. Kempe kjeder har vist seg instrumental i farging og re-farging grafer. Se Figur 1. Det ville være en forbløffende forenkling hvis Birkhoff-diamanten alene er nøkkelen til 4-colourability. Det første gyldige beviset ble kunngjort i 1976 Av Kenneth Appel Og Wolfgang Haken. Det kreves over tusen timer datamaskin tid for å verifisere bestemte aspekter av deres argument. Denne forestillingen om å stole på datakode, som potensielt inneholder menneskeskapte feil (og deres kode gjorde!), i stedet for et ‘menneskelig’ bevis, har ikke tilfredsstilt en stor del av det matematiske samfunnet. Appel Og Haken bevis var elegant i sin overordnede struktur, men detaljene var stygge. beviset ble raffinert i 1996 av et team av fire matematikere: Robertson, Sanders, Seymour og Thomas, men de stolte fortsatt på datakode for å fullføre sitt bevis. I 2010 tilbød Steinberger en annen variasjon. Det er imidlertid fortsatt ikke noe helt tilfredsstillende svar på hvorfor 4-fargeteoremet er sant. (Når formodningen ble bevist, fikk den status som en teorem.’)

søket etter et alternativt bevis
4-fargeproblemet er så lett å artikulere og forstå at det har tiltrukket interessen til mange tusen amatørmatematikere, alle tror de kan finne et enkelt klassisk bevis og dermed bli kjent. Jim Tilleys far, fysiker og rektor Ved Canadas Royal Military College fra 1978-1984, var en slik drømmer. Når han følte at han hadde gjort et gjennombrudd, ville han be sin sønn, Jim, for å sjekke sitt arbeid. Jim har alltid funnet en feil. Likevel, til tross for sin første skepsis til at farens innsats noen gang ville bære frukt, ble han smittet med en entusiasme for 4-fargeproblemet og begynte å studere det intensivt.Jim Tilleys forskning førte til at Han oppdaget en ny eiendom som et minimums moteksempel på 4-fargesetningen må vise. Han kalte Det Kempe-locking. Han innså at det var sannsynlig å være uforenlig med en annen eiendom som et minimum counterexample må vise-nemlig., hvor tilkoblet en graf er (hvor mange hjørner må fjernes fra en graf før den faller fra hverandre).

Tilleys kempe-låsing er en egenskap forbundet med en kant i en triangulasjon. Begrepet starter med å slette en kant xy mellom tilstøtende hjørner x og y. Hvis for hver 4-farging av den resulterende grafen der fargene på x og y er de samme, er det ingen sekvens av fargeutvekslinger på Kempe-kjeder som får fargen på x til å avvike fra fargen på y, så sies den opprinnelige trianguleringen Å Være Kempe-låst med hensyn til kanten xy. Tilley viste at et minimum moteksempel til 4-fargeteoremet må Være Kempe-låst med hensyn til hver eneste kant; hver kant i et minimum moteksempel må ha denne fargeegenskapen.

Kempe-låsing er en spesielt restriktiv tilstand som blir vanskeligere å tilfredsstille når en triangulering blir større. Tilley satt ut for å finne ut om det er noe felles for trianguleringer som har Kempe-låste kanter. Hans tidligste søk Etter kempe-låsing førte ham til Birkhoff-diamanten.

Birkhoff-diamanten
I 1913 oppdaget Gd Birkhoff at en viss konfigurasjon av ti land i et kart (en grensering av seks land som omslutter et sett med fire land) har en viktig egenskap. Hvis den konfigurasjonen er til stede i et kart, og hvis submap med den konfigurasjonen fjernet er 4-colourable, vil hele kartet være 4-colourable. Dermed kan et minimum moteksempel ikke inneholde den bestemte konfigurasjonen. Den er kjent som Birkhoff-diamanten. Tilley fant at En Kempe-låst kant xy synes å oppstå bare når x og y er også endepunktene i grafen versjon Av En Birkhoff diamant. Se Figur 2.

formodningen er lett uttalt, forståelig og spennende, og gir en overbevisende forklaring på hvorfor alle plan grafer er 4-farger. Han hadde ikke møtt Noen kempe-låsekonfigurasjon uten En Birkhoff-diamant, og antok at Birkhoff-diamanten er den eneste ‘grunnleggende’ kempe-låsekonfigurasjonen, en som ikke inneholder en mindre kempe-låsekonfigurasjon som en undergraf. Imidlertid Fant Tilley at Han ikke kunne bevise sin kritiske formodning. Det var frustrerende fordi, hvis sant, ville formodningen direkte bevise 4-fargesetningen. (For å være et minimum moteksempel, må en triangulering inneholde En Birkhoff diamant subgraph, men hvis det gjorde det, kunne det ikke være et minimum moteksempel.)

en overveldende støtte sak
I Stedet for å bevise sin formodning, Tilley gjorde det nest beste. Han bestemte seg for å spille rollen som en eksperimentalist og bygge en overveldende sak for å støtte sin formodning. Han delte alle relevante plan trianguleringer i to klasser: de der minst fire hjørner må fjernes før grafene faller fra hverandre (4-tilkoblet) og de der minst fem hjørner må fjernes før grafene faller fra hverandre (5-tilkoblet). Se Figur 3. Nyttig I Tilleys omfattende søk var at Han måtte undersøke bare ett medlem av hver isomorfisme klasse (grafer som er strukturelt identiske). Tilley undersøkte alle 8,044 isomorfisme klasser av 4-tilkoblede plan trianguleringer på opptil 15 hjørner og alle 9,733 isomorfisme klasser av 5-tilkoblede plan trianguleringer på opptil 24 hjørner. Han fant bare tre kempe-låste trianguleringer. Hver oppdaget Kempe-låst kant inneholdt En Birkhoff diamant og hver skjedde i en 4-tilkoblet triangulering. Det var ingen i det hele tatt blant 5-tilkoblede trianguleringer.

Tilley utvidet sitt søk blant 4-tilkoblede trianguleringer ved å undersøke alle 30 926 isomorfisme klasser på 16 hjørner og alle 158 428 isomorfisme klasser på 17 hjørner. Beregningstidsbegrensninger betydde å begrense søket til prøver på 100 000 tilfeldig genererte ikke-isomorfe trianguleringer hver for klasser på 18,19 og 20 hjørner. Det utvidede søket viste 45 ekstra kempe-låste trianguleringer, men nøyaktig de samme resultatene som det opprinnelige søket: hver kempe-låst kant i en triangulering inneholdt en tilhørende Birkhoff-diamant.

hvor herfra? Tilleys omfattende søk bekreftet lett at Birkhoff-diamanten er en grunnleggende kempe-låsekonfigurasjon. Han har grundig testet sin formodning, men det er fortsatt uprøvd. Hvis (eller når) Tilleys formodning er bevist sant, det vil si At Birkhoff-diamanten alene er nøkkelen til 4-colourability, ville Det være en forbløffende forenkling av problemet: en enkelt konfigurasjon som forklarer alt-matematisk eleganse –

Beviser 4-farge formodning kreves innsatsen til mange fremtredende matematikere. Tilleys formodning om At Birkhoff-diamanten er den eneste grunnleggende kempe-låsekonfigurasjonen, kan være enda vanskeligere å bevise. Det eksperimentelle beviset er imidlertid sterkt. Teoretikere kan si ‘ hvorfor bry?»Tilleys svar er at umettelig nysgjerrighet vil vinne ut: «tross alt er formodningen lett oppgitt, forståelig og spennende, og gir en overbevisende forklaring på hvorfor alle plan grafer er 4-farger.»