Rational Exponents
Rational Exponents
Learning Objective(s)
· Convert radicals to expressions with rational exponents.
· Convert expressions with rational exponents to their radical equivalent.
· Use the laws of exponents to simplify expressions with rational exponents.
· Use rational exponents to simplify radical expressions.
Introduksjon
Kvadratrøtter er oftest skrevet med et radikalt tegn, som dette, ![]() . Men det er en annen måte å representere å ta en rot på. Du kan bruke rasjonelle eksponenter i stedet for en radikal. En rasjonell eksponent er en eksponent som er en brøkdel. For eksempel kan
. Men det er en annen måte å representere å ta en rot på. Du kan bruke rasjonelle eksponenter i stedet for en radikal. En rasjonell eksponent er en eksponent som er en brøkdel. For eksempel kan ![]() skrives som
skrives som ![]() .Kan du ikke forestille deg å heve et tall til en rasjonell eksponent? De kan være vanskelig å bli vant til, men rasjonelle eksponenter kan faktisk bidra til å forenkle noen problemer. La oss utforske forholdet mellom rasjonelle (fraksjonelle) eksponenter og radikaler.
.Kan du ikke forestille deg å heve et tall til en rasjonell eksponent? De kan være vanskelig å bli vant til, men rasjonelle eksponenter kan faktisk bidra til å forenkle noen problemer. La oss utforske forholdet mellom rasjonelle (fraksjonelle) eksponenter og radikaler.
Omskriving Av Radikale Uttrykk Ved Hjelp Av Rasjonelle Eksponenter
Radikaler og fraksjonelle eksponenter er alternative måter å uttrykke det samme på. Du har allerede sett hvordan firkantede røtter kan uttrykkes som en eksponent for kraften til en halv.
|
Radical Form |
Exponent Form |
Integer |
|
|
|
4 |
|
|
|
5 |
|
|
|
10 |
Let’s look at some more examples, but this time with cube roots. Husk at kubing av et tall øker det til kraften til tre. Legg merke til at i disse eksemplene er nevneren til den rasjonelle eksponenten tallet 3.
|
Radical Form |
Exponent Form |
Integer |
|
|
|
2 |
|
|
|
5 |
|
|
|
10 |
These examples help us model a relationship between radicals and rasjonelle eksponenter: nemlig at den nte roten til et tall kan skrives som enten ![]() eller
eller ![]() .
.
|
Radical Form |
Exponent Form |
|
|
|
|
|
|
|
|
|
|
… |
… |
|
|
|
When faced with an uttrykk som inneholder en rasjonell eksponent, du kan omskrive den ved hjelp av en radikal. I tabellen ovenfor legger du merke til hvordan nevneren til den rasjonelle eksponenten bestemmer rotenes indeks. Så, en eksponent for ![]() oversetter til kvadratroten, en eksponent for
oversetter til kvadratroten, en eksponent for ![]() oversetter til den femte roten eller
oversetter til den femte roten eller ![]() og
og ![]() oversetter til den åttende roten eller
oversetter til den åttende roten eller ![]() .
.
|
Example |
||
|
Problem |
Write |
|
|
|
The radical form |
|
|
Answer |
|
|
|
Example |
||
|
Problem |
Express |
|
skriv om uttrykket med brøkeksponenten som en radikal. Nevneren av fraksjonen bestemmer roten, i dette tilfellet kuben rot. parentesene i |
Svar |
|
husk at eksponenter bare refererer til antallet umiddelbart til venstre med mindre et grupperingssymbol brukes. Eksemplet nedenfor ser veldig ut som det forrige eksemplet med en viktig forskjell-det er ingen parenteser! Se hva som skjer.
|
Example |
||
|
Problem |
Express |
|
|
|
Rewrite the expression with the fractional exponent as a radical. Nevneren av fraksjonen bestemmer roten, i dette tilfellet kuben rot. eksponenten refererer bare til delen av uttrykket umiddelbart til venstre for eksponenten, i dette tilfellet x, men ikke 2. |
|
|
Answer |
|
|
Rewriting Expressions with Rational Exponents Using Radicals
Just as you can rewrite an expression with a rational exponent as a radical expression, you can express a radical expression using a rational exponent.
|
Example |
||
|
Problem |
Express |
|
|
|
Rewrite the radical using a rational exponent. The root determines the fraction. I dette tilfellet er indeksen for radikalet 3, så den rasjonelle eksponenten vil være siden 4 er utenfor radikalet, er det ikke inkludert i grupperingssymbolet, og eksponenten refererer ikke til det. |
|
|
Answer |
|
|
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the expression with the fractional exponent as a radical. |
|
|
6 • x2 |
Find the square root of both the coefficient and the variable. |
Svar |
|
rasjonelle eksponenter med andre tellere enn en
alle tellerne for brøkeksponentene i eksemplene ovenfor var 1. Du kan bruke brøkeksponenter som har andre tellere enn 1 for å uttrykke røtter, som vist nedenfor. Legg merke til noen mønstre i denne tabellen?
|
Radical |
Exponent |
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
… |
|
|
|
for å omskrive en radikal ved hjelp av en brøkdel eksponent, blir kraften som radikanden heves til telleren og roten blir nevneren.
Skrive Brøk Eksponenter
enhver radikal i form ![]() kan skrives ved hjelp av en brøk eksponent i form
kan skrives ved hjelp av en brøk eksponent i form ![]() .
.
forholdet mellom![]() og
og ![]() fungerer for rasjonelle eksponenter som også har en teller på 1. For eksempel kan den radikale
fungerer for rasjonelle eksponenter som også har en teller på 1. For eksempel kan den radikale ![]() også skrives som
også skrives som ![]() , siden et hvilket som helst tall forblir den samme verdien hvis den heves til den første strømmen. Du kan nå se hvor telleren på 1 kommer fra i tilsvarende form av
, siden et hvilket som helst tall forblir den samme verdien hvis den heves til den første strømmen. Du kan nå se hvor telleren på 1 kommer fra i tilsvarende form av ![]() .
.
Forenkle Radikale Uttrykk Ved Hjelp Av Rasjonelle Eksponenter og Eksponentens Lover
la oss utforske noen radikale uttrykk nå og se hvordan du kan forenkle dem. Her er et radikalt uttrykk som trenger forenkling, ![]() .
.
en metode for å forenkle dette uttrykket er å faktor og trekke ut grupper av a3, som vist nedenfor i dette eksemplet.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite by factoring out cubes. |
|
|
|
Write each factor under its own radical and simplify. |
|
|
Svar |
|
|
du kan også forenkle dette uttrykket ved å tenke på det radikale som et uttrykk med en rasjonell eksponent, og bruke prinsippet om at enhver radikal i form ![]() kan skrives med en brøkdel eksponent i skjemaet
kan skrives med en brøkdel eksponent i skjemaet![]() .
.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the radical using a rational exponent. |
|
|
|
Simplify the exponent. |
|
|
Answer |
|
|
Note that rational exponents are subject to all of the same rules as other exponents when they appear in algebraic expressions.
begge forenklingsmetodene ga samme resultat, a2. Avhengig av problemets sammenheng kan det være lettere å bruke en metode eller den andre, men for nå vil du merke at du kunne forenkle dette uttrykket raskere ved hjelp av rasjonelle eksponenter enn ved bruk av» uttrekksmetoden».
la oss prøve et annet eksempel.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the radical using rational exponents. Use the rules of exponents to simplify the expression. |
|
|
|
||
|
|
Change the expression with the rasjonell eksponent tilbake til radikal form. |
Svar |
|
igjen er den alternative metoden å jobbe med å forenkle under radikalet ved å bruke factoring. For eksemplet du nettopp løste, ser det slik ut.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the expression. |
|
|
|
Factor each radicand. |
|
|
|
Simplify. |
|
|
Answer |
|
|
Which of the expressions below is equal to the expression ![]() when written using a rational exponent?
when written using a rational exponent?
A) ![]()
B) ![]()
C)![]()
D) ![]()
la oss prøve et mer komplisert uttrykk, ![]() . Dette uttrykket har to variabler, en brøkdel og en radikal. La oss ta det trinnvis og se om bruk av brøkdelte eksponenter kan hjelpe oss med å forenkle det.
. Dette uttrykket har to variabler, en brøkdel og en radikal. La oss ta det trinnvis og se om bruk av brøkdelte eksponenter kan hjelpe oss med å forenkle det.
la oss begynne med å forenkle nevnen, siden dette er hvor det radikale tegnet er plassert.
|
Example |
|||
|
Problem |
Simplify. |
||
|
|
Separate the factors in the denominator. |
||
|
|
Take the cube root of 8, which is 2. |
||
|
|
|
Rewrite the radical using a fractional exponent. |
|
|
|
Rewrite the fraction as a series of factors in order to cancel factors (see next step). |
||
|
|
Simplify the constant and c factors. |
||
|
|
Use the rule of negative exponents, n-x= |
||
|
|
Combine the b factors by adding the exponents. |
||
|
|
Change the expression with the fractional exponent back to radical form. Ved konvensjon anses et uttrykk vanligvis ikke forenklet hvis det har en brøkdel eksponent eller en radikal i nevnen. |
||
|
Svar |
|
||
vel, det tok en stund, men du gjorde det. Du brukte det du vet om fraksjonelle eksponenter, negative eksponenter og eksponentens regler for å forenkle uttrykket.
Sammendrag
en radikal kan uttrykkes som et uttrykk med en brøk eksponent ved å følge konvensjonen ![]() . Omskriving av radikaler ved hjelp av fraksjonelle eksponenter kan være nyttig for å forenkle noen radikale uttrykk. Når du arbeider med brøkeksponenter, husk at brøkeksponenter er underlagt alle de samme reglene som andre eksponenter når de vises i algebraiske uttrykk.
. Omskriving av radikaler ved hjelp av fraksjonelle eksponenter kan være nyttig for å forenkle noen radikale uttrykk. Når du arbeider med brøkeksponenter, husk at brøkeksponenter er underlagt alle de samme reglene som andre eksponenter når de vises i algebraiske uttrykk.
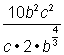
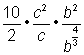
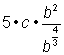
Leave a Reply