grafen for en lineær ulikhet i en variabel er en tallinje. Bruk en åpen sirkel for < og > og en lukket sirkel for ≤ og ≥.

grafen for x> -3

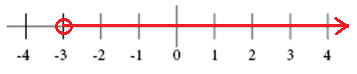
grafen for x ≥ 2

Ulikheter som har Ulikheter som har samme løsning kalles ekvivalent. Det er egenskaper av ulikheter, så vel som det var egenskaper av likestilling. Alle eiendommene nedenfor gjelder også for ulikheter som involverer ≥

addisjonsegenskapen til ulikhet sier at å legge det samme tallet til hver side av ulikheten gir en ekvivalent ulikhet

$$If \: x>y,\: then\: x+z>y+z$

$$If\: x<y,\: deretter\: x + z <y + z$$

subtraksjonsegenskapen til ulikhet forteller oss at å trekke det samme tallet fra begge sider av en ulikhet gir en ekvivalent ulikhet.

$$Hvis \: x>y,\: deretter\: x-z>y-z$$

$$Hvis\: X<y,\: deretter\: x-z<y-z$$

multiplikasjonsegenskapen til ulikhet forteller oss at multiplikasjon på begge sider av en ulikhet med et positivt tall gir en ekvivalent ulikhet.

$$Hvis \: x>y\: og\: z>0,\: deretter\: xz>yz$$

$Hvis\: X<y\: og\: z>0,\: deretter\: xz<yz$$

multiplikasjon i hver side av en ulikhet med et negativt tall på den annen side gir ikke en ekvivalent ulikhet med mindre vi også reverserer Retningen Av Ulikhetssymbolet

$$if \: x>y \: og\: z<0,\: deretter\: xz<yz$$

$$hvis\: x<y\: og\: z < 0,\: deretter\: xz >yz$ $

det samme gjelder for divisjonsegenskapen til ulikhet.

Divisjon av begge sider av en ulikhet med et positivt tall gir en ekvivalent ulikhet.

$$Hvis \: x>y \: og\: z>0,\: deretter\: \frac{x}{z}>\frac{y}{z}$$

$$Hvis\: x<y\: og\: z>0,\: deretter\: \frac{x}{z}<\frac{y}{z}$$

og divisjon på begge sider av en ulikhet med et negativt tall gir en ekvivalent ulikhet hvis ulikhetssymbolet reverseres.

$$Hvis \: X>y \: og\: z<0,\: deretter\: \frac{x}{z}<\frac{y}{z}$$

$$Hvis\: x<y\: og\: z<0,\: deretter\: \frac{x}{z}>\frac{y}{z}$$

for å løse en flertrinns ulikhet gjør du som du gjorde når du løste flertrinns ligninger. Ta en ting om gangen helst ved å isolere variabelen fra konstantene. Når man løser ulikheter i flere trinn, er det viktig å ikke glemme å reversere ulikhetstegnet når man multipliserer eller deler med negative tall.

Eksempel

Løs ulikheten

$$-2 \ venstre (x + 3 \ høyre ) <10$ $