komplekse tall: introduksjon (side 1 av 3)

seksjoner: Introduksjon, operasjoner med komplekser, kvadratisk formel

frem til nå har du blitt fortalt at du ikke kan ta kvadratroten av et negativt tall. Det er fordi du ikke hadde noen tall som var negative etter at du hadde kvadrert dem (slik at du ikke kunne «gå bakover» ved å ta kvadratroten). Hvert tall var positivt etter at du kvadrerte det. Så du kunne ikke veldig godt kvadratroten en negativ og forventer å komme opp med noe fornuftig.

Nå kan du imidlertid ta kvadratroten av et negativt tall, men det innebærer å bruke et nytt tall for å gjøre det. Dette nye nummeret ble oppfunnet (oppdaget ? rundt Reformasjonstiden. På den tiden trodde ingen at noen «ekte verden» bruk ville bli funnet for dette nye nummeret, annet enn å lette beregningene involvert i å løse visse ligninger, så det nye nummeret ble sett på som et late nummer oppfunnet for enkelhets skyld.

(Men så, når du tenker på det, er ikke alle tall oppfinnelser? Det er ikke som tall vokser på trær! De lever i hodene våre. Vi fant dem alle opp! Hvorfor ikke finne en ny, så lenge det fungerer bra med det vi allerede har?)

> nå kan du tro at du kan gjøre dette:

men dette gir ingen mening! Du har allerede to tall som kvadratet til 1; nemlig -1 og + 1. Og jeg har allerede kvadrater til -1. Så det er ikke rimelig at jeg også vil kvadrat til 1. Dette peker på en viktig detalj: Når du arbeider med fantasi, får du noe (evnen til å håndtere negativer i firkantede røtter), men du mister også noe (noen av fleksibiliteten og praktiske regler du pleide å ha når du arbeider med firkantede røtter). Spesielt MÅ DU ALLTID GJØRE i-DELEN først!

• Forenkle sqrt(-9). Copyright © Elizabeth Stapel 2000-2011 Alle Rettigheter Reservert

(Advarsel: trinnet som går gjennom det tredje «lik» tegnet er » «, ikke ««. Jeg er utenfor det radikale.)

• Forenkle sqrt(-25).

• Forenkle sqrt(-18).

• Forenkle –sqrt(-6).

i beregningene dine vil du håndtere jeg akkurat som du ville med x, bortsett fra at x2 bare er x2, men i2 er -1:

• Forenkle 2i + 3i.

2i + 3i = (2 + 3)I = 5i

• forenkle 16i – 5i.

16i – 5i = (16 – 5)i = 11i

• Multiplisere og forenkle (3i)(4i).

(3i) (4i) = (3 * 4) (i·i) = (12) (i2) = (12)(-1) = -12

• Multipliser Og forenkle (i)(2i)(–3i).

(i)(2i) (- 3i) = (2 · -3) (i · i * i) = (-6) (i2 · i)

=(-6) (-1 · i) = (-6) (–i) = 6i

Merk dette siste problemet. Innenfor det kan du se at , fordi i2 = -1. Fortsetter, vi får:

dette mønsteret av krefter, tegn, 1 og jeg er en syklus:

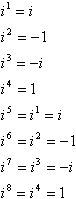
Med andre ord, for å beregne noen høy effekt av i, kan du konvertere den til en lavere effekt ved å tar det nærmeste multiplum av 4 som ikke er større enn eksponenten og trekker dette multiplum fra eksponenten. For eksempel er et vanlig lurespørsmål på tester noe i tråd med «Forenkle i99», ideen er at du vil prøve å multiplisere jeg nitti ni ganger, og du vil gå tom for tid, og lærerne vil få en god fnise på bekostning av deg i fakultetets salong. Slik fungerer snarveien:

i99 = i96 + 3 = i (4×24)+3 = i3 = –i

Det vil si i99 = i3, fordi du bare kan lop av i96. (Nittiseks er et flertall på fire, så i96 er bare 1, som du kan ignorere.) Med andre ord kan du dele eksponenten med 4 (ved hjelp av lang divisjon), kaste bort svaret, og bruk bare resten. Dette vil gi deg den delen av eksponenten du bryr deg om. Her er noen flere eksempler:

• Forenkle i17.

i17 = i16 + 1 = i4 · 4 + 1 = i1 = i

• Forenkle i120.

i120 = i4 · 30 = i4· 30 + 0 = i0= 1

• Forenkle i64,002.

i64,002 = i64,000 + 2 = i4 · 16,000 + 2 = i2 = –1

Top | 1 | 2 | 3 | Return to Index Next >>