Fibonacci-Sekvensen
Fibonacci-Sekvensen er serien av tall:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …
det neste tallet er funnet ved å legge sammen de to tallene før det:
- 2 er funnet ved å legge til de to tallene før det (1+1),
- 3 er funnet ved å legge til de to tallene før det (1+2),
- 5 er (2+3),
- og så videre!
Eksempel: det neste tallet i sekvensen ovenfor er 21+34 = 55
det er så enkelt!
her er en lengre liste:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, …
Kan du finne ut de neste tallene?
Lager En Spiral
Når vi lager firkanter med disse breddene, får vi en fin spiral:

ser du hvordan rutene passer pent sammen?
for eksempel 5 og 8 gjør 13, 8 og 13 gjør 21, og så videre.

denne spiralen finnes i naturen!
Se: Natur,Det Gylne Snitt og Fibonacci
Regelen
Fibonacci-Sekvensen kan skrives som En» Regel » (Se Sekvenser og Serier).
for Det Første er vilkårene nummerert fra 0 og utover som dette:
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | … |
| xn = | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | … |
så term nummer 6 kalles x6 (som tilsvarer 8).
|
Eksempel: 8. term er x8 = x7 + x6 |
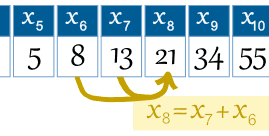 |
så vi kan skrive regelen:
regelen er xn = xn−1 + xn−2
hvor:
- xn er term nummer «n»
- xn−1 er forrige term (n−1)
- xn−2 er termen før det (n−2)
Eksempel: term 9 beregnes slik:
gylne snitt

og her er en overraskelse. Når vi tar to påfølgende (den ene etter den andre) Fibonacci-Tall, er deres forhold svært nær Det Gyldne Forholdet «φ» som er omtrent 1.618034…
In fact, the bigger the pair of Fibonacci Numbers, the closer the approximation. Let us try a few:
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
2
|
3
|
1.5 | |
|
3
|
5
|
1.666666666… | |
|
5
|
8
|
1.6 | |
|
8
|
13
|
1.625 | |
|
…
|
…
|
… | |
|
144
|
233
|
1.618055556… | |
|
233
|
377
|
1.618025751… | |
|
…
|
…
|
… |
vi trenger ikke å starte med 2 og 3, her valgte jeg tilfeldig 192 og 16 (og fikk sekvensen 192, 16, 208, 224, 432, 656, 1088, 1744, 2832, 4576, 7408, 11984, 19392, 31376, …):
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
192
|
16
|
0.08333333… | |
|
16
|
208
|
13 | |
|
208
|
224
|
1.07692308… | |
|
224
|
432
|
1.92857143… | |
|
…
|
…
|
… | |
|
7408
|
11984
|
1.61771058… | |
|
11984
|
19392
|
1.61815754… | |
|
…
|
…
|
… |
det tar lengre tid å få gode verdier, men det viser at Ikke Bare Fibonacci-Sekvensen kan gjøre dette!
Bruke Det Gylne Snitt til Å Beregne Fibonacci-Tall
Og enda mer overraskende er at Vi kan beregne Hvilket Som helst Fibonacci − Tall ved Å bruke Det Gylne Snitt:
xn = φn−(1-φ)n√5
svaret kommer ut som et helt tall, nøyaktig lik tilsetningen av de to foregående begrepene.
Eksempel: x6
x6 = (1.618034…)6 − (1−1.618034…)6√5
da jeg brukte en kalkulator på dette (bare inn I Golden Ratio til 6 desimaler) fikk jeg svaret 8.00000033, en mer nøyaktig beregning ville være nærmere 8.
Prøv n = 12 og se hva du får.
Du kan også beregne Et Fibonacci-Tall ved å multiplisere Det forrige Fibonacci-Tallet med Det Gylne Snitt og deretter avrunde (fungerer for tall over 1):
Eksempel: 8 × φ = 8 × 1.618034… = 12.94427… = 13 (avrundet)
Noen Interessante Ting
Her Er Fibonacci-sekvensen igjen:
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | … |
| xn = | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 | … |
Det er et interessant mønster:
- Se på tallet x3 = 2. Hvert 3. tall er et multiplum av 2 (2, 8, 34, 144, 610, …)
- Se på tallet x4 = 3. Hvert 4. tall er et multiplum av 3 (3, 21, 144,…)
- Se på tallet x5 = 5. Hvert 5. tall er et multiplum av 5 (5, 55, 610,…)
Og så videre (hvert nte tall er et multiplum av xn).
1/89 = 0.011235955056179775…
Legg Merke til De første sifrene (0,1,1,2,3,5) Er Fibonacci-sekvensen?
På en måte er de alle, bortsett fra flere tall (13, 21, etc) overlapper hverandre, slik som dette:
… osv …
0.011235955056179775… =1/89
Vilkår Under Null
sekvensen fungerer under null også slik:
| n= | … | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| xn = | … | −8 | 5 | −3 | 2 | −1 | 1 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | … |
(Bevis for deg selv at hvert tall er funnet ved å legge sammen de to tallene før det!)
faktisk har sekvensen under null de samme tallene som sekvensen over null, bortsett fra at de følger en +-+- … mønster. Det kan skrives slik:
x−n = (-1)n+1 xn
Som sier at termen «−n» er lik (-1)n+1 ganger termen «n», og verdien (-1) n + 1 gjør det riktig +1, -1, +1, -1, … mønster.
Historie
Fibonacci var ikke den første som visste om sekvensen, den var kjent i India hundrevis av år før!

Om Fibonacci Mannen
Hans virkelige navn Var Leonardo Pisano Bogollo, og han bodde mellom 1170 og 1250 I Italia.
«Fibonacci» var hans kallenavn, som grovt betyr «Sønn Av Bonacci».i tillegg til Å være kjent For Fibonacci-Sekvensen, hjalp han med å spre Hindu-arabiske Tall (som våre nåværende tall 0, 1, 2, 3, 4, 5, 6, 7, 8, 9) Gjennom Europa i stedet For Romerske Tall(I, II, III, IV, V, etc). Det har spart oss alle for mye trøbbel! Takk Leonardo.

Fibonacci-Dag
Fibonacci-Dag er 23.November, da Den har sifrene «1, 1, 2, 3» som er en del av sekvensen. Så neste November 23 la alle vite!
Leave a Reply