Articles

Easy Permutations and Combinations

by admin

jeg har alltid forvirret «permutasjon» og «kombinasjon» – hvilken er hvilken?

Her er en enkel måte å huske: permutasjon høres komplisert, ikke sant? Og det er det. Med permutasjoner betyr hver liten detalj. Alice, Bob og Charlie er forskjellig Fra Charlie, Bob og Alice(sett inn dine venners navn her).

Kombinasjoner, derimot, er ganske enkle å gå. Detaljene spiller ingen rolle. Alice, Bob Og Charlie er Det Samme Som Charlie, Bob Og Alice.

Permutasjoner er for lister (ordreforhold) og kombinasjoner er for grupper (rekkefølge spiller ingen rolle).

Du vet, en «kombinasjonslås» burde virkelig bli kalt en «permutasjonslås». Ordren du legger tallene i saker.

Enkle Permutasjoner og Kombinasjoner

en sann «kombinasjonslås» vil akseptere både 10-17-23 og 23-17-10 som korrekt.

Permutasjoner: de hårete detaljene

la oss starte med permutasjoner, eller alle mulige måter å gjøre noe på. Vi bruker fancy-bukser begrepet «permutasjon» , så vi kommer til å bry seg om hver minste detalj, inkludert rekkefølgen på hvert element. La oss si at vi har 8 personer: 

1: Alice2: Bob3: Charlie4: David5: Eve6: Frank7: George8: Horatio

Hvor mange måter kan vi tildele en 1., 2. og 3. plass blant åtte deltakere? (Gull / Sølv / Bronse)

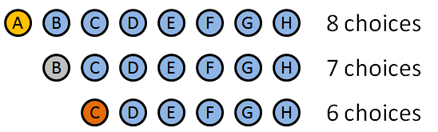
permuation eksempel medaljer

Vi kommer til å bruke permutasjoner siden rekkefølgen vi dele ut disse medaljene saker. Her er Hvordan det bryter ned:

  • Gullmedalje: 8 valg: A B C D E F G H (Smart hvordan jeg gjorde navnene samsvarer med bokstaver, eh ?). La Oss si at A vinner Gullet.
  • Sølvmedalje: 7 valg: B C D E F G H. La Oss si At B vinner sølv.
  • Bronsemedalje: 6 valg: C D E F G H. La oss si … C vinner bronse.

vi valgte bestemte personer til å vinne, men detaljene spiller ingen rolle: vi hadde 8 valg først, deretter 7, deretter 6. Det totale antall alternativer var $8 * 7 * 6 = 336$.

La oss se på detaljene. Vi måtte bestille 3 personer ut av 8. For å gjøre dette startet vi med alle alternativene (8) og tok dem bort en om gangen (7, deretter 6) til vi gikk tom for medaljer.

vi vet at faktorialet er:

\displaystyle{ 8! = 8 \ cdot 7 \ cdot 6 \ cdot 5 \ cdot 4 \ cdot 3 \cdot 2 \ cdot 1 }

Dessverre gjør Det for mye! Vi vil bare ha $8 * 7 * 6$. Hvordan kan vi «stoppe» fakultetet ved 5?

dette er hvor permutasjoner blir kule: legg merke til hvordan vi vil bli kvitt $5 * 4 * 3 * 2 * 1$. Hva er et annet navn for dette? 5 faktoriell!

Så, hvis vi gjør 8!/5! vi får:

\ displaystyle {\frac{8!}{5!} = \frac{8 \ cdot 7 \ cdot 6 \ cdot 5 \ cdot 4 \ cdot 3 \ cdot 2 \cdot 1}{5 \cdot 4 \ cdot 3 \ cdot 2 \ cdot 1} = 8 \cdot 7 \cdot 6}

Og hvorfor brukte vi tallet 5? Fordi det var igjen etter at vi plukket 3 medaljer fra 8. Så en bedre måte å skrive dette på ville være:

\ displaystyle {\frac{8!}{(8-3)!}}

var 8!/(8-3)! er bare en fancy måte å si » Bruk de første 3 tallene på 8!”. Hvis vi har n elementer totalt og vil velge k i en bestemt rekkefølge, får vi:

\ displaystyle{\frac{n!{(n-k)!}}

og dette er den fancy permutasjonsformelen: Du har n elementer og vil finne antall måter k elementer kan bestilles på:

\displaystyle{P(n,k) = \frac{n!{(n-k)!}}

Kombinasjoner, Ho!

Kombinasjoner er enkle å gå. Orden spiller ingen rolle. Du kan blande det opp og det ser det samme ut. La oss si at jeg er en cheapskate og ikke har råd til separate Gull -, Sølv-og Bronsemedaljer. Faktisk har jeg bare råd til tomme blikkbokser.

Hvor mange måter kan jeg gi 3 bokser til 8 personer?

Vel, i dette tilfellet, rekkefølgen vi plukke folk spiller ingen rolle. Hvis Jeg gir en boks Til Alice, Bob og Deretter Charlie, er det det samme som Å gi Til Charlie, Alice og Deretter Bob. Uansett er de like skuffet.

Dette reiser et interessant poeng-vi har noen oppsigelser her. Alice Bob Charlie = Charlie Bob Alice. For et øyeblikk, la oss bare finne ut hvor mange måter vi kan omorganisere 3 personer.

Vel, vi har 3 valg for den første personen, 2 for den andre og bare 1 for den siste. Så vi har $3 * 2 * 1$ måter å re-arrangere 3 personer.

Vent litt … dette ser litt ut som en permutasjon! Du lurte meg!

Det gjorde jeg. Hvis Du har n folk og du vil vite hvor mange ordninger det er for dem alle, er det bare n factorial eller N!

Så, hvis vi har 3 blikkbokser å gi bort, er det 3! eller 6 variasjoner for hvert valg vi velger. Hvis vi vil finne ut hvor mange kombinasjoner vi har, lager vi bare alle permutasjonene og deler av alle oppsigelsene. I vårt tilfelle får vi 336 permutasjoner (ovenfra), og vi deler med 6 redundanser for hver permutasjon og får 336/6 = 56.

den generelle formelen er

\displaystyle{C(n,k) = \frac{P (n,k)}{k!}}

som betyr » Finn alle måtene å plukke k folk fra n, og del med k! variant”. Når vi skriver dette ut, får vi vår kombinasjonsformel, eller antall måter å kombinere k elementer fra et sett med n:

\displaystyle{C(n,k) = \frac{n!{(n-k)!k!}}

Noen Ganger er C(n,k) skrevet som:

\displaystyle {\binom {n}{k}}

som er binomialkoeffisienten.

noen eksempler

Her er noen eksempler på kombinasjoner (rekkefølge spiller ingen rolle) fra permutasjoner (ordenssaker).

  • Kombinasjon: Plukke et team av 3 personer fra en gruppe på 10. $C (10,3) = 10!/(7! * 3!) = 10 * 9 * 8 / (3 * 2 * 1) = 120$.

    Permutasjon: Plukke En President, VP Og Waterboy fra en gruppe på 10. $P(10,3) = 10!/7! = 10 * 9 * 8 = 720$.

  • Kombinasjon: Velge 3 desserter fra en meny med 10. C (10,3) = 120.

    Permutasjon: Oppgi dine 3 favoritt desserter, i rekkefølge, fra en meny med 10. P (10,3) = 720.

ikke husk formlene, forstå hvorfor de fungerer. Kombinasjoner høres enklere enn permutasjoner, og de er. Du har færre kombinasjoner enn permutasjoner.

Andre Innlegg i Denne Serien

  1. Enkle Permutasjoner og Kombinasjoner
  2. Navigere I Et Rutenett Ved Hjelp Av Kombinasjoner og Permutasjoner
  3. Hvordan Forstå Kombinasjoner Ved Hjelp Av Multiplikasjon
  4. Hvorfor multipliserer vi kombinasjoner?