en kraft kan betraktes som en push orpull i en bestemt retning. Når en kraft påføres et objekt, avhenger den resulterende bevegelsen av objektet av hvor kraften påføres og hvordan objektet er begrenset.Hvis objektet er ubegrenset og kraften påføres gjennomtyngdepunktet, beveger objektet seg i puretranslation, som beskrevet Av Newtons bevegelseslover.Hvis objektet er begrenset (eller festet) på et sted kalt apivot, objectrotatesom pivot, men oversetter ikke.Kraften overføres gjennom svingetog detaljene i rotasjonen avhenger av avstanden fraden påførte kraften til svinget.Hvis objektet er ubegrenset og kraften påføres på noenavstand fra tyngdepunktet, oversetter objektet begge delerog roterer om tyngdepunktet.Detaljer om rotasjonen avhenger av avstanden frapåført kraft til tyngdepunktet.Bevegelsen av flygende objekter erbeskrevet av denne tredje typen bevegelse; en kombinasjon av oversettelse og rotasjon.

en kraft F Er avektorantall, noe som betyr at den har både en størrelse ogen retning knyttet til den. Retning av kraftener viktig fordi den resulterende bevegelsen av objekteter i samme retning som kraften.Produktet av kraften og den vinkelrette avstanden til tyngdepunktet for et ubestemt objekt, eller til svinget for et begrenset objekt, er^Mcalled dreiemomentet eller øyeblikket.Et dreiemoment er også en vektormengde og produserer en rotasjonpå samme måte som en kraft produserer en oversettelse. Nemlig, et objekt atrest, eller roterer med en konstant vinkelhastighet, vil fortsette å gjøre sountil det er underlagt et eksternt dreiemoment. Et dreiemoment gir en endringi vinkelhastighet som kalles en vinkelakselerasjon.

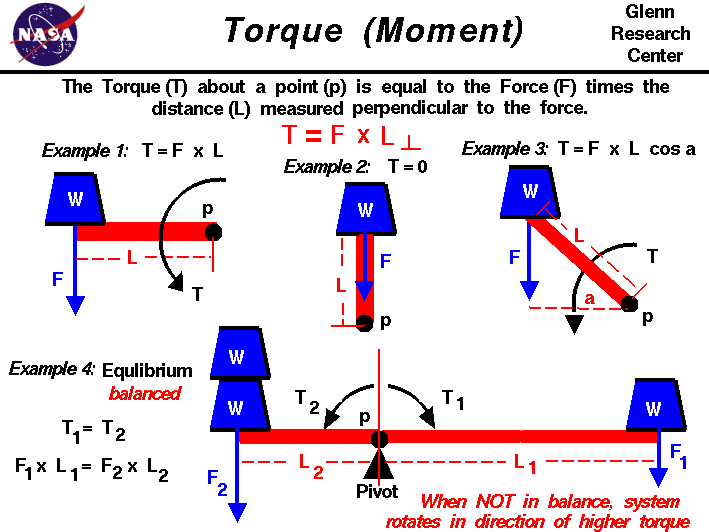
avstanden L brukes til å bestemme dreiemomentet T er avstanden frapivot p til kraften, men målt vinkelrett påretning av kraften.På figuren viser vi fire eksempler på momenter for å illustrere det grunnleggendeprinsipper som styrer torques.In hvert eksempel en blå vekt W virker på en rød bar, som kallesen arm.

I Eksempel 1 blir kraften (vekten) påført vinkelretttil armen. I dette tilfellet er den vinkelrette avstanden lengden påstang og dreiemomentet er lik produktet av lengden og kraften.

I Eksempel 2 brukes den samme kraften på armen, men kraften virker nå rett gjennompivot. I dette tilfellet er avstanden fra svinget vinkelrett på kraftener null. Så i dette tilfellet er dreiemomentet også null.Tenk på en hengslet dør. Hvis du trykker på kanten av døren, mot hengslet, beveger døren seg ikke fordi dreiemomentet er null.

Eksempel 3 Er det generelle tilfellet der kraften påføresi noen vinkel a tilarmen. Den vinkelrette avstanden er gitt avtrigonometrysom lengden av armen (L) ganger thecosine (cos) av vinkelen.Dreiemomentet er da gitt av:

Eksempler 1 og 2 kan utledes fra denne generelle formelen,sidenkosin av0 grader er 1,0 (Eksempel 1), og cosinus av 90 grader er 0,0 (Eksempel 2).

i Eksempel 4 er pivoten flyttet fra enden av stolpen til en plassering nær midten av stolpen. Vekter legges til begge siderav pivot.To høyre en enkeltvekt W produserer en kraft F1 som virkeri en avstand L1 fra pivoten. Dette skaper et dreiemoment T1 likprodukt av kraften og avstanden.

til venstre forpivot to vekter w produserer en kraft F2 på en avstand L2.Dette produsereret dreiemoment T2 i en retning motsatt Fra T1 fordi avstandener i motsatt retning.

hvis systemet var i likevekt,eller balansert, ville dreiemomentet være lik og ingen netto dreiemoment ville virke på systemet.

hvis systemet ikke er i likevekt, eller ubalansert, roterer barenom svinget i retning av høyere dreiemoment.Hvis F2 = 2 * F1, hva er forholdet Mellom L1 Og L2 for å balansere systemet? Hvis F2 = 2 * F1 Og L1 = L2, i hvilken retning vil systemet rotere?Aeronautical ingeniører bruker dreiemomentet generert av aerodynamiske overflater for å stabilisere og kontrollere fly.På fly produserer kontrollflateneaerodynamiske krefter.Disse kreftene påføres i noen avstand frafly cg og derforforårsake flyet å rotere. Theelevators produsere apitching øyeblikk, therudder produsere ayawing øyeblikk, og theailerons produsere arolling øyeblikk. Evnen til å variere mengden avkraften og øyeblikket tillater piloten å manøvrere eller totrim flyet.På modellraketter, denfinsbrukes til å generere et dreiemoment om rocketcenter of gravityfor å gistabilitetunder drevet flytur.På drager, de aerodynamiske og vektkrefterprodusere et dreiemoment omtridlepunkt.Avstanden fra hodepunktet og størrelsen påkrefter har en sterk effekt påytelsenav draken.

Aktiviteter:
Knappen For Å Vise Klasse 11-12 Aktivitetdiv>guidede turer

• krefter, dreiemoment og bevegelse:
• grunnleggende flybevegelse:

Fly Roll Bevegelse: fly pitch bevegelse:

• fly yaw bevegelse:

Balanseror: spoilers:

• heiser:

stabilatorer:

• Ror:

Stabilitet Av en modell rakett:

navigasjon..

nybegynners guide home page