Definitive Integraler
Du vil kanskje lese Introduksjon til Integrasjon først!
Integrasjon
|
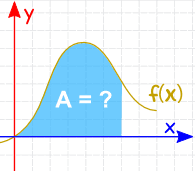
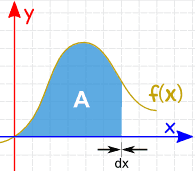
Integrasjon kan brukes til å finne områder, volumer, sentrale punkter og mange nyttige ting. Men det brukes ofte til å finne området under grafen til en funksjon som dette: |
|
området kan bli funnet ved å legge til skiver som nærmer seg null i bredde: og Det er Integrasjonsregler som hjelper oss med å få svaret. |
Notasjon
symbolet for «integral» er en stilig «s» (for «sum», ideen om å summere skiver):
etter integral symbolet setter vi funksjonen vi vil finne integralet av (kalt integranden).
og avslutt deretter med dx for å bety at skivene går i x-retningen (og nærmer seg null i bredden).
Bestemt Integral
Et Bestemt Integral har start-og sluttverdier: med andre ord er det et intervall .
a og b (kalt grenser, grenser eller grenser) settes på bunnen og toppen av «S», slik:
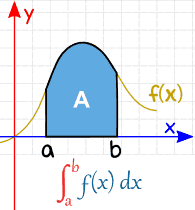 |
 |
|
| Definite Integral (from a to b) |
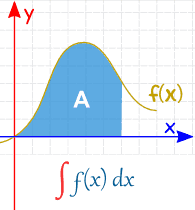
Indefinite Integral (no specific values) |
We find the Definite Integral by calculating the Indefinite Integral at a, and at b, then subtracting:
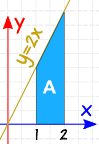
Eksempel: Hva er 2 ∫ 1 2x Dx
Vi blir bedt om Det Bestemte Integralet, fra 1 til 2, av 2x Dx
først må vi finne Ubestemt Integral.
Ved Hjelp Av Integreringsreglene finner vi at ∫2x dx = x2 + C
beregner nå at ved 1 og 2:
- ved x=1: ∫2x dx = 12 + C
- ved x=2: ∫2x dx = 22 + C
Trekker:
Og «C» blir kansellert … så Med Bestemte Integraler kan vi ignorere C.
Resultat:
1

sjekk: med en så enkel form, la oss også prøve å beregne området etter geometri:
a = 2+42 × 1 = 3
Ja, det har et areal på 3.
(Yay!)
Notasjon: Vi kan vise ubestemt integral (uten +C) i firkantede parenteser, med grensene a og b etter, slik:
Eksempel (fortsatt)
en god måte å vise svaret ditt på:
=
= 22 − 12
la oss prøve et annet eksempel:
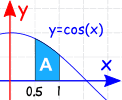
Example:
The Definite Integral, from 0.5 to 1.0, of cos(x) dx:
(Note: x must be in radians)
The Indefinite Integral is: ∫cos(x) dx = sin(x) + C
We can ignore C for definite integrals (as we saw above) and we get:
=
And another example to make an important point:
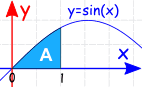
Example:
The Definite Integral, from 0 to 1, of sin(x) dx:
0
sin(x) dx
det Ubestemte Integralet er:∫sin(x) dx = −cos(x) + c
siden vi går fra 0, kan vi bare beregne integralet ved x=1?
– cos (1) = -0.540…
Hva? Er det negativt? Men det ser positivt ut i grafen.
Vel … vi gjorde en feil!
Fordi vi må trekke integralet ved x=0. Vi bør ikke anta at det er null.
så la oss gjøre det riktig, trekke den ene fra den andre:
0
sin(x) dx =
= −cos(1) − (−cos(0))
Det er bedre!
Men vi kan ha negative regioner, når kurven er under aksen:

Eksempel:
Det Bestemte Integralet, fra 1 til 3, av cos(x) dx:
Legg Merke Til at noe av det er positivt, og noe negativt.
det bestemte integralet vil regne ut nettoverdien.
la oss gjøre beregningene:
=
= sin(3) − sin(1)
Hopp det er mer negativt enn positivt med nettoresultatet av -0.700….
så vi har denne viktige tingen å huske:
prøv å integrere cos(x) med forskjellige start-og sluttverdier for å se selv hvordan positive og negative fungerer.
Positivt Område
Men noen ganger vil vi at alt område skal behandles som positivt(uten at delen under aksen trekkes fra).
i så fall må vi beregne områdene separat, som i dette eksemplet:

Eksempel: Hva er det totale arealet mellom y = cos (x) og x-aksen, fra x = 1 til x = 3?
dette er som eksemplet vi nettopp gjorde, men nå forventer vi at alt område er positivt (tenk at vi måtte male det).
så nå må vi gjøre delene separat:
- En for området over x-aksen
- En for området under x-aksen
kurven krysser x-aksen ved x = π/2 så vi har:
fra 1 til π/2:
= sin(π/2) − sin(1)
fra ④ /2 til 3:
= sin(3) − sin(π/2)
Den siste kommer ut negativ, men vi vil at den skal være positiv, så:
Totalt areal = 0,159… + 0.859… = 1.018…
dette er veldig forskjellig fra svaret i forrige eksempel.
Kontinuerlig
Å ja, funksjonen vi integrerer må Være Kontinuerlig mellom a og b: ingen hull, hopp eller vertikale asymptoter (hvor funksjonen går opp/ned mot uendelig).
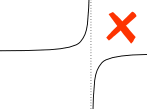
Eksempel:
en vertikal asymptote mellom a og b påvirker det bestemte integralet.
Egenskaper
Område over − område under
integralet legger til området over aksen, men trekker området under, for en «nettoverdi»:
f(x) dx = (Område over x − aksen) – (Område under x-aksen)
Legge Til Funksjoner
integralet av f+g er lik integralet av f pluss integralet av g:
f(x) + g(x) dx =
f(x) dx +
a g(x) dx
reversere intervallet
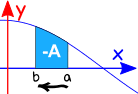
reversering av intervallets retning gir negativet av den opprinnelige retningen.
![]()

Leave a Reply