Math Er mer av en maraton enn en sprint — det er en lang, langsom og jevn grind, med sjeldne øyeblikk av gjennombrudd. Likevel, en gang imellom, får vi de dyrebare «Eureka» – øyeblikkene, de korte linjene med bokstaver og tall som forandrer vitenskapen for alltid. Her er noen av de mest kjente ligningene, fra de gamle Grekerne til moderne fysikk.

Pythagoras teorem (530 F. KR.)

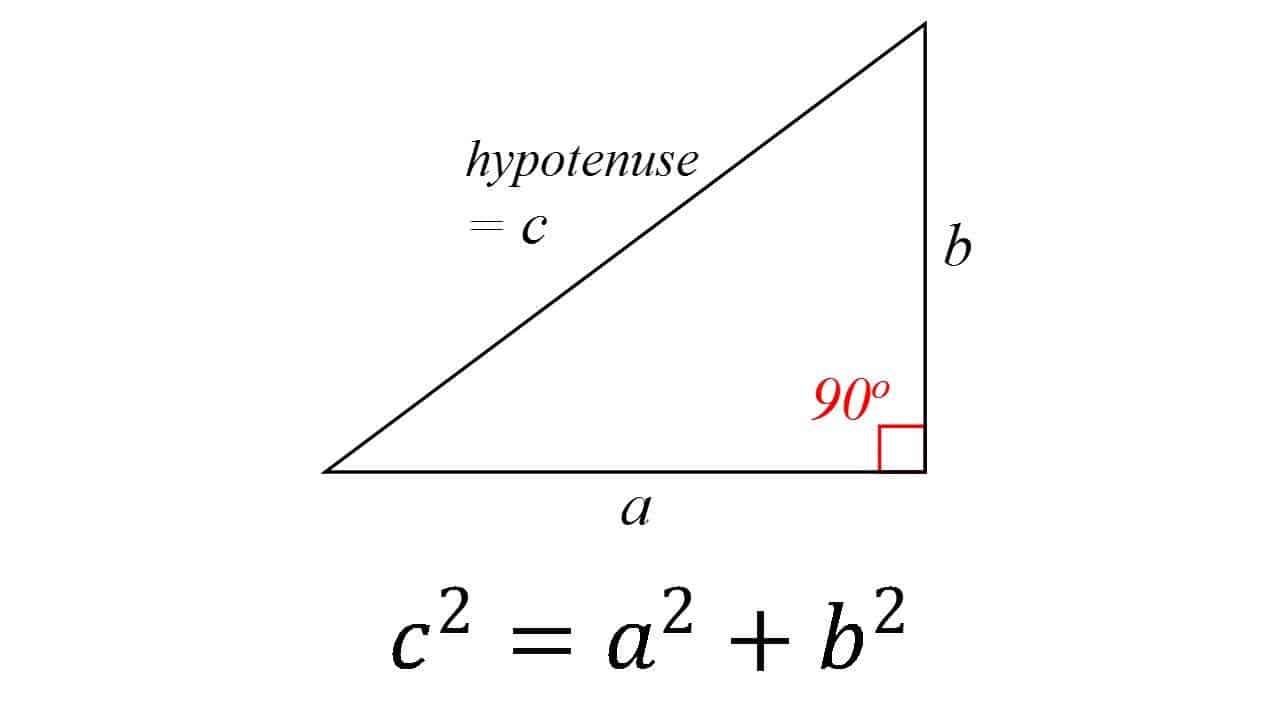
Dette er ganske en av de grunnleggende pilarene alle geometri: i en høyre trekant er kvadratet av hypotenusen (siden motsatt den rette vinkelen) lik summen av kvadratene til de andre to. Teorien er generelt tilskrevet den greske matematikeren Pythagoras, selv om det er noen bevis for At Babylonske matematikere forstått formelen. Det er også veldig mulig at teoremet var kjent av mange mennesker, men han var den første til å bevise det.

teoremet har fått mange bevis-muligens mest for noen matematisk teorem. De er svært mangfoldig, inkludert både geometriske bevis og algebraiske bevis, med noen dating tilbake tusenvis av år.

Komplekse tall

Den italienske matematikeren Gerolamo Cardano er den første kjente Som har introdusert komplekse tall, og kaller dem «fiktive» på den tiden. Den matematiske utviklingen av » jeg » som det imaginære tallet som representerer kvadratroten av -1 tilskrives Leonhard Euler, En Av de viktigste matematikere og forskere i menneskets historie.Komplekse tall Er i utgangspunktet tall som egentlig ikke eksisterer, men som er svært nyttige for en rekke beregninger. De består av tall med en reell del (tallene vi alle vet) og en imaginær del (jeg representerte her) og har praktiske anvendelser på mange felt, inkludert fysikk, kjemi, biologi, økonomi, elektroteknikk og statistikk.

logaritmene

Logaritmer er i utgangspunktet den inverse funksjonen av eksponering. Du trenger et tall (N), en base (a), og logaritmen Til n i base a vil være x, Hvor N er lik a til kraften til x. Det kan virke som bare en annen måte å skrive det samme på (og på en måte er det), men logaritmer har et myriade av praktiske applikasjoner, som brukes i psykologi, økonomi og målinger av mange fysiske fenomener (som pH eller jordskjelvstørrelse).Logaritmer ble offentlig fremmet av John Napier i 1614 i en bok med tittelen Mirifici Logarithmorum Canonis Descriptio (Beskrivelse Av Logaritmenes Vidunderlige Regel) — en passende tittel. Et spesielt tilfelle av logaritmen er den naturlige logaritmen-e, hvor e er et irrasjonelt og transcendentalt tall omtrent lik 2.71828182845. Faktisk har e selv en fascinerende historie og et imponerende antall applikasjoner, men det er en historie for en annen gang.

Kalkulus

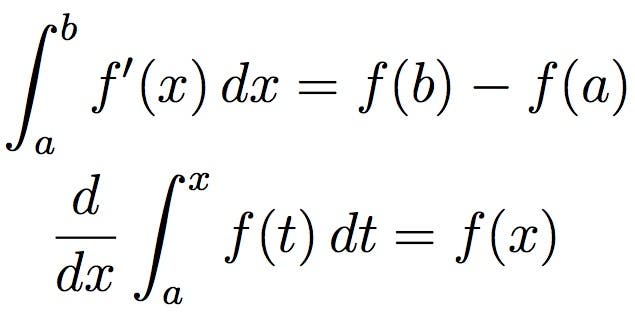
Få felt av matematikk har vært like virkningsfulle som kalkulus. Utviklet I Det 17. århundre Av Isaac Newton Og Gottfried Wilhelm Leibniz, er kalkulus mye brukt i vitenskap, ingeniørfag og økonomi. Kalkulus fokuserer vanligvis på å håndtere små mengder, spesielt uendelig små mengder. Gjennom kalkulator kan disse behandles som reelle tall, selv om de er teknisk uendelig små.

for en enklere visualisering kan integrasjon, avbildet ovenfor, betraktes som å måle området under en kurve, definert av en funksjon.

Tyngdeloven

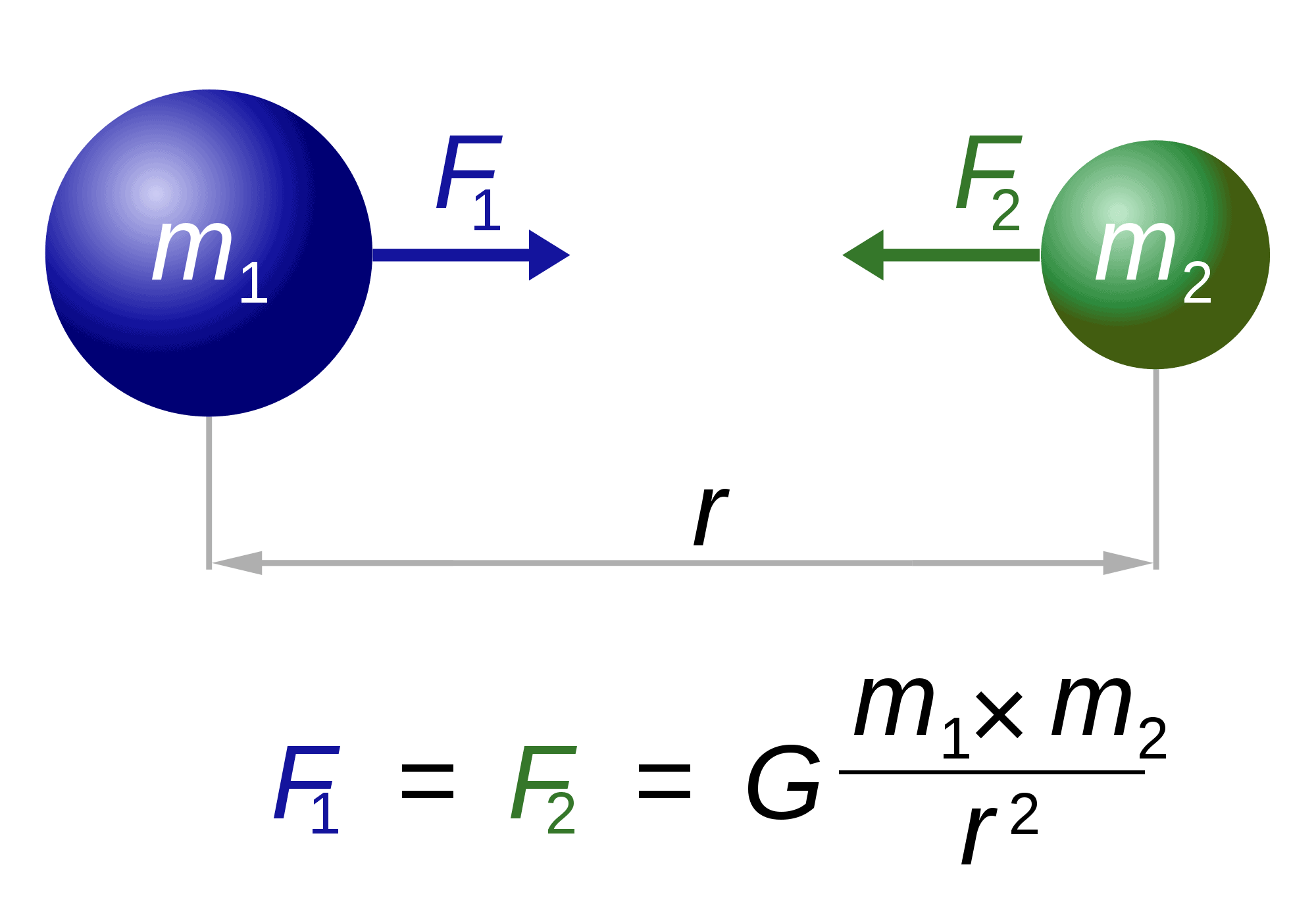
Når Det Gjelder Newton, er Han også «ansvarlig» for en av verdens mest berømte og spektakulære ligninger: tyngdeloven.Loven beskriver i utgangspunktet hvordan to legemer av massene m1 og m2 er tiltrukket av hverandre. Kraften (F1, F2) er omvendt proporsjonal med kvadratet av avstanden mellom dem (r). Den eneste gjenværende faktoren, G, er en gravitasjonskonstant. Naturen til denne konstanten forblir unnvikende.

Generell Relativitet

I nesten 200 år definerte Newtons lov vårt nivå av forståelse av mekanikk. Einsteins arbeid i det 20.århundre tok ting til neste nivå — disse to prestasjonene tårner på de høyeste piedestalene i fysikkens verden.Generell relativitet er i hovedsak en geometrisk gravitasjonsteori, som generaliserer Newtons teori og gir en enhetlig beskrivelse av tyngdekraften som en geometrisk egenskap av rom og tid — eller romtid. Spesielt Viste Einstein ikke bare at det er en ting som» spacetime » som fusjonerer de tre dimensjonene med 4. dimensjon av tid, men han viste også at denne spacetime kan bøyes av tyngdekraften, med krumningen som er direkte relatert til energi og momentum av uansett materie og stråling er tilstede.

Termodynamikkens Andre lov

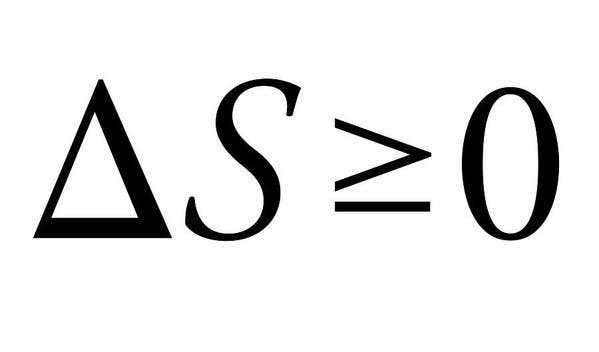
Termodynamikkens Andre Lov er hvorfor Vi ikke kan ha fine ting i Universet. Vitser til side, de fire lovene i termodynamikk definerer grunnleggende fysiske mengder (temperatur, energi og entropi) som karakteriserer termodynamiske systemer. Den andre, spesielt, skiller seg ut her på grunn av sin enkelhet, men absolutt massive implikasjoner.loven sier i hovedsak at summen av entropiene til de interagerende termodynamiske systemene alltid må øke, eller i det meste forbli konstant. Når energi endres fra en form til en annen eller materie beveger seg rundt, øker entropien (eller lidelsen) i et lukket system. Alle forskjeller i temperatur, trykk og tetthet har en tendens til å flate ut etter en stund

Maxwells Ligninger

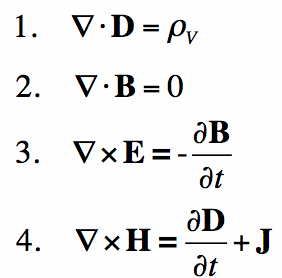
Enkelt Sagt, Maxwells ligninger er til elektromagnetisme Hva Newtons lov er til mekanikk. De gir et matematisk grunnlag for klassisk elektromagnetisme, klassisk optikk og elektriske kretser. De er mye brukt i selve enheten du leser dette på-i utgangspunktet alle elektroniske enheter.Maxwells lover beskriver hvordan elektriske og magnetiske felt genereres av ladninger, strømmer og endringer i feltene. Et betydelig gjennombrudd var demonstrasjonen som elektriske og magnetiske felt forplanter seg ved lysets hastighet.

Eulers Identitet

Til Slutt Er dette ganske muligens den mest elegante ligningen, en ting av høyeste skjønnhet, fordi den involverer alle de «grunnleggende» tallene:

• 0, som er nøytral for addisjon og subtraksjon;
• 1, som er nøytral for multiplikasjon og divisjon;
• e, som er eulers tall (Se Ovenfor), basen av naturlige logaritmer;
• i er den imaginære enheten (se ovenfor); og
• π er pi, forholdet mellom omkretsen av en sirkel til dens diameter.

Å Finne et forhold som forener alle disse tallene er intet mindre enn fantastisk, og virker ganske usannsynlig. Demonstrasjonen er ikke akkurat enkel, men du kan se den her.Det er bare passende At Matematikkprofessor Keith Devlin ved Stanford University beskrev ligningen og sa at»som En Shakespeare — sonett som fanger selve essensen av kjærlighet, eller et maleri som bringer frem skjønnheten i den menneskelige formen som er langt mer enn bare huddyp, når eulers ligning ned i selve eksistensens dyp» Det er ikke ofte at matematikk og fysikk koker ned til enkle og elegante ligninger-men når De gjør det, er Det litt av et syn å se.