Evaluering Av Cohen’ S Kappa

verdien for kappa kan være mindre enn 0 (negativ). En score på 0 betyr at det er tilfeldig avtale mellom raters, mens en score på 1 betyr at det er en fullstendig avtale mellom raters. Derfor betyr en poengsum som er mindre enn 0 at det er mindre avtale enn tilfeldig sjanse. Nedenfor vil jeg vise deg formelen for å finne ut av dette, men det er viktig at du gjør deg kjent med figur 4 for å ha en sterk forståelse.

figur 4: N x n grid brukes til å tolke resultatene av raters

grunnen til at jeg uthevet to nett vil bli klart i et øyeblikk, men for nå, la meg bryte ned hvert rutenett.

A = > det totale antall tilfeller som begge raters sa var riktige. Raterne er enige.

B = > det totale antall tilfeller Som Rater 2 sa var feil, Men Rater 1 sa var riktige. Dette er en uenighet.

C = > det totale antall tilfeller Som Rater 1 sa var feil, Men Rater 2 sa var riktige. Dette er også en uenighet.

D = > det totale antall tilfeller som Begge Raters sa var feil. Raters er enige.

for å kunne utarbeide kappa-verdien må vi først vite sannsynligheten for avtale (dette forklarer hvorfor jeg fremhevet avtalediagonalen). Denne formelen er avledet ved å legge til antall tester der raters er enige og deretter dele den med totalt antall tester. Ved å bruke eksemplet fra figur 4, ville det bety (A + D)/(A + B+ C+ D).

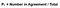
Figur 5: sannsynlighet for avtale

perfekt! Det neste trinnet er å regne ut sannsynligheten for tilfeldig avtale. Ved hjelp av figur 4 som en guide, er forventet verdi det totale antall ganger Som Rater 1 sa riktig dividert med totalt antall forekomster, multiplisert med totalt antall ganger Som Rater 2 sa riktig dividert med totalt antall forekomster, lagt til det totale antall ganger Som Rater 1 sa feil multiplisert med totalt antall ganger Som Rater 2 sa feil. Det er mye informasjon å ta inn der, så i figur 6 har jeg formulert denne ligningen ved hjelp av rutenettet ovenfor.

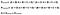
Lastly, the formula for Cohen’s Kappa is the probability of agreement take away the probability of random agreement divided by 1 minus the probability of random agreement.

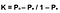
Flott! Du er nå i stand til å skille mellom pålitelighet og gyldighet, forklare Cohens kappa og evaluere det. Denne statistikken er veldig nyttig, men siden jeg har forstått hvordan det fungerer, tror jeg nå at det kan være underutnyttet når man optimaliserer algoritmer til en bestemt metrisk. I Tillegg Gjør Cohen ‘ s kappa også en god jobb med å måle både flerklasse og ubalanserte klasseproblemer.

P. S. Hvis Det er noe du vil at Jeg skal dekke Med Datavitenskap, kan du sende meg melding På Twitter @ KurtisPykes Eller legge igjen et svar på dette innlegget.