bevaring av momentum er et grunnleggende konsept for fysikksammen medbevaring av energiog bevaring av masse.Momentum er definert til å være massen av et objekt multiplisert med hastigheten av objektet.Bevaringen av momentum sier at, innenfor et problemdomene, forblir mengden momentum konstant;momentum er verken skapt eller ødelagt, men bare endretgjennom virkningen av krefter som beskrevet Av Newtons bevegelseslover.Å håndtere momentum er vanskeligere enn å håndtere masse og energi fordi momentum er avektor quantityhawing både en størrelse og en retning. Momentum er bevart i alle trefysiske retninger samtidig. Det er enda vanskeligere når det gjelder agasfordi krefter i en retning kan påvirke momentumet i en annen retningpå grunn av kollisjoner av mange molekyler.På dette lysbildet presenterer vi et veldig, veldig forenklet flytproblemhvor egenskaper bare endres i en retning.Problemet forenkles ytterligere ved å vurdere en jevn strøm som ikke endres med tiden og ved å begrense kreftene til bare de som er forbundet med thepressure.Be klar over at ekte flytproblemer er myemer komplekseenn dette enkleeksempel.

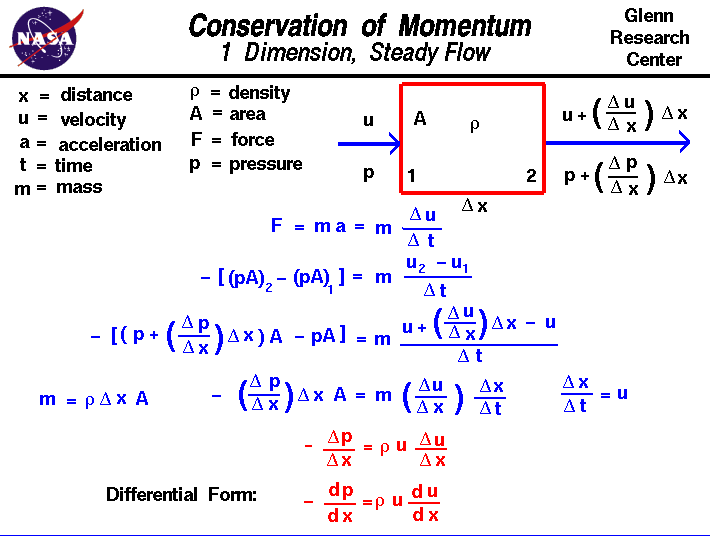
la oss vurdere strømmen av en gass gjennom et domene der strømningsegenskaperbare endre i en retning, som vi vil kalle «x». Gassen går inn i domainat stasjon 1 med en viss hastighet u og en viss trykkpand går ut på stasjon 2 med en annen valueof hastighet og trykk. For enkelhet vil vi anta dettettheten r forblir konstant innenfor domenetog at området A gjennom hvilket gassen strømmer også forblir konstant. Plasseringen av stasjonene 1 og 2 er skiltmed en avstand kalt del x. (Delta er den lille trekanten på glidenog er det greske bokstaven «d». Matematikere bruker ofte dette symbolet til å betegne endring eller variasjon av en mengde. Web print font støtter ikkede greske bokstavene, så vi vil bare kalle det «del».) En endring med avstand er referert til som en gradientfor å unngå forvirring med en endring med tiden som kalles en hastighet.Hastighetsgradienten er angitt med del u / del x; endringen i hastighet perchange i avstand. Så på stasjon 2 er hastigheten gitt av hastighetenpå 1 pluss gradienten ganger avstanden.

et lignende uttrykk gir trykketved utgangen:

Newtons andre bevegelseslov sier at kraften F er lik endringen i momentum medrespekt på tid. For et objekt med konstant massm dette reduserer til masse ganger akselerasjon a.An accelerasjon er en endring i hastighet med endring i tid (del u / del t). Deretter:

kraften i dette problemetkommer fra trykkgradienten. Siden trykk er en kraft per arealenhet, er nettokraften på vårt fluiddomene trykk ganger området vedutgang minus trykk ganger området ved inngangen.

minustegnet påbegynnelsen av dette uttrykket brukes fordi gasser beveger seg fra en regionhøyt trykk til et område med lavt trykk; hvis trykket øker medx, vil hastigheten reduseres. Erstatte våre uttrykk for hastighetog trykk:

Forenkle:

Å Merke seg at (del x / del t) er hastighet og at massen er tettheten r ganger volumet (område ganger del x):

forenkle:

Del p / del x og del u / del x representerer trykk-og hastighetsgradientene.Hvis vi krymper vårt domene ned til differensialstørrelser, blir disse gradientene differensialer:

Dette er en endimensjonal, stabil form avulers Equation.It er interessant å merke seg at trykkfalletav en væske (termen til venstre) er proporsjonal med både verdien avveiehastigheten og hastighetsgradienten.En løsning av denne momentumligningen gir oss formen avdynamisk trykk som vises inbernoullis Ligning.

Aktiviteter:
Guidede Turer

• Grunnleggende Fluiddynamikkligninger:

Navigasjon ..

Nybegynners Guide Home Page