beanz Magazine
Kart av Merian-Erben (1652) På Wikipedia
denne månedens mattepuslespill går tilbake til 1735 da Det først ble løst Av Leonhard Euler, En Sveitsisk matematiker og fysiker.
puslespillet kalles De Syv Broene I K Hryvnigsberg. Den er basert på en faktisk by, deretter I Preussen, nå Kaliningrad I Russland. Byen er delt av en elv med to øyer i mellom og, lenger nedstrøms, elven deler byen igjen.
problemet er villedende enkelt: Det er (eller var, i Eulers tid) syv broer for å koble de to øyene og nedstrøms deler av byen. Euler lurte på om en person kunne gå over hver av de syv broene en gang og bare en gang for å berøre alle deler av byen. Start og slutt på samme sted var ikke et krav.
Her er et kart du kan bruke til å prøve å løse problemet for deg selv:
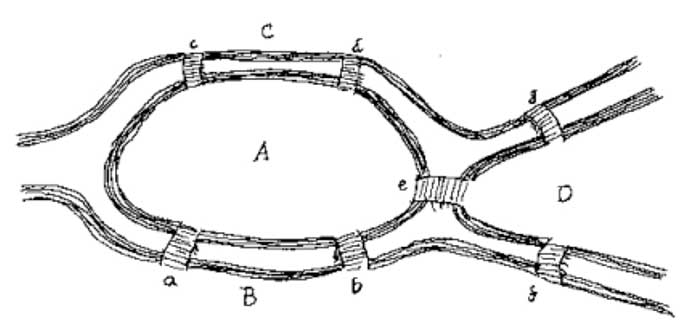
hva tror du er mer viktig å løse dette problemet: antall broer eller plasseringen av hver bro?
Svar: antall broer.
Euler beviste at antall bruer må være et partall, for eksempel seks bruer i stedet for syv, hvis du ønsker å gå over hver bro en gang og reise til Hver del Av K Hryvnigsberg. Løsningen ser hver bro som et endepunkt, et toppunkt i matematiske termer, og forbindelsene mellom hver bro (toppunkt). Euler innså at bare et jevnt antall broer ga det riktige resultatet av å kunne berøre alle deler av byen uten å krysse en bro to ganger.
Euler brukte matematikk for å bevise at det var umulig å krysse alle syv broer bare en gang og besøke Alle deler Av Kö. Ved å gjøre det satte han i gang en rekke funn og innsikt om hvordan rom og kryssende mellomrom kan defineres, så vel som deres egenskaper. En detaljert beskrivelse Av eulers løsning i Wikipedia-lenken under denne artikkelen.Hvis du noen gang har sett en mobius-stripe, har du for eksempel sett et eksempel på topologi, et matematisk fagområde utviklet Seg fra Eulers løsning på dette problemet. Topologi er opptatt av plass og hvordan ting knytter seg til hverandre, samt kontinuitet og grenser for rom. Topologi studerer også hvordan egenskapene til et rom endres og ikke endres når rommet er utvidet eller kontrahert.i databehandling er topologi nyttig for å forstå nettverkene (banene) data kan flyte i ethvert system, samt hvordan datasett kan forholde seg til hverandre. De Syv Broene I K Hryvnigsberg ligner også på et annet vanlig databehandlingsproblem som noen ganger kalles Reiseselgerproblemet der du prøver å finne den mest effektive ruten gitt et sett med restriksjoner som de syv broene i Eulers problem.Ikke-matematikere (sannsynligvis du, definitivt meg) opplever Reiseselgerproblemet når vi kommer på tog eller buss. Den Reiser Selger Problemet er å finne ut den mest effektive måten å reise mellom par av byer av angitte avstander. Administrere knappe ressurser (tog, busser) som reiser langs begrensede ruter er et perfekt problem for databehandling å løse fordi datamaskiner er raskere og mer effektive. Men Først trenger Vi Euler og andre til å oppgi problemet og definere løsninger med matte. Vi programmerer deretter våre datamaskiner for å gjøre matematikken.Topologi omhandler også mengdelære, hvordan grupper av ting kan sorteres i sett for å identifisere felles elementer med andre grupper, samt unike elementer. Et Venn-diagram er et godt eksempel på et sett. Og programmering må noen ganger sortere data på forskjellige måter. Hvilken sorteringsmetode som fungerer best for en situasjon, kan bestemmes av settteori.
Og hva skjedde med de syv broene Fra Eulers tid? To broer ble revet og erstattet med en enkelt motorvei. Av de tre gjenværende broene ble den ene gjenoppbygd i 1935, mens De to andre forblir intakte Slik Euler kjente dem. Og Selvfølgelig har Königsberg, Preussen endret navn Til Kaliningrad, Russland.
Leave a Reply