Energetikk Av Ionisk Bindingsdannelse

Ioniske bindinger dannes når positivt og negativt ladede ioner holdes sammen av elektrostatiske krefter. Tenk på et enkelt par ioner, en kation og en anion. Hvor sterk vil kraften i deres tiltrekning være? Ifølge Coulombs Lov er energien til den elektrostatiske attraksjonen (\(E\)) mellom to ladede partikler proporsjonal med ladningens størrelse og omvendt proporsjonal med internukleær avstand mellom partiklene (\(r\)):

\

\

hvor hver ionladning representeres Av symbolet Q. proporsjonalitetskonstanten k er lik 2.31 × 10-28 j * m. denne verdien av k inkluderer ladningen av et enkelt elektron (1.6022 × 10-19 C) for hver ion. Ligningen kan også skrives ved hjelp av ladningen til hver ion, uttrykt i coulombs (C), innlemmet i konstanten. I dette tilfellet er proporsjonalitetskonstanten, k, lik 8.999 × 109 j * m / C2. I eksemplet gitt, Q1 = +1(1.6022 × 10-19 C) Og Q2 = -1(1.6022 × 10-19 C). Hvis Q1 og Q2 har motsatte tegn (som I NaCl, for eksempel Hvor Q1 er + 1 For Na+ og Q2 er -1 For Cl−), er E negativ, noe som betyr at energi frigjøres når motsatt ladede ioner bringes sammen fra en uendelig avstand for å danne et isolert ionpar.

Energi frigjøres alltid når en binding dannes, og tilsvarende krever det alltid energi for å bryte en binding.

som vist ved den grønne kurven i Den nedre halvdelen Av Figur \(\PageIndex{1}\), vil maksimal energi frigjøres når ionene er uendelig nær hverandre, ved r = 0. Fordi ioner opptar plass og har en struktur med den positive kjernen omgitt av elektroner, kan de imidlertid ikke være uendelig tett sammen. På svært korte avstander blir repulsive elektron-elektron-interaksjoner mellom elektroner på tilstøtende ioner sterkere enn de attraktive interaksjonene mellom ioner med motsatte ladninger, som vist ved den røde kurven i Den øvre halvdelen Av Figur \(\PageIndex{1}\). Den totale energien i systemet er en balanse mellom de attraktive og frastøtende interaksjoner. Den lilla kurven I Figur \(\PageIndex{1}\) viser at systemets totale energi når et minimum ved r0, punktet der de elektrostatiske avstøtningene og attraksjonene er nøyaktig balansert. Denne avstanden er den samme som den eksperimentelt målte bindingsavstanden.

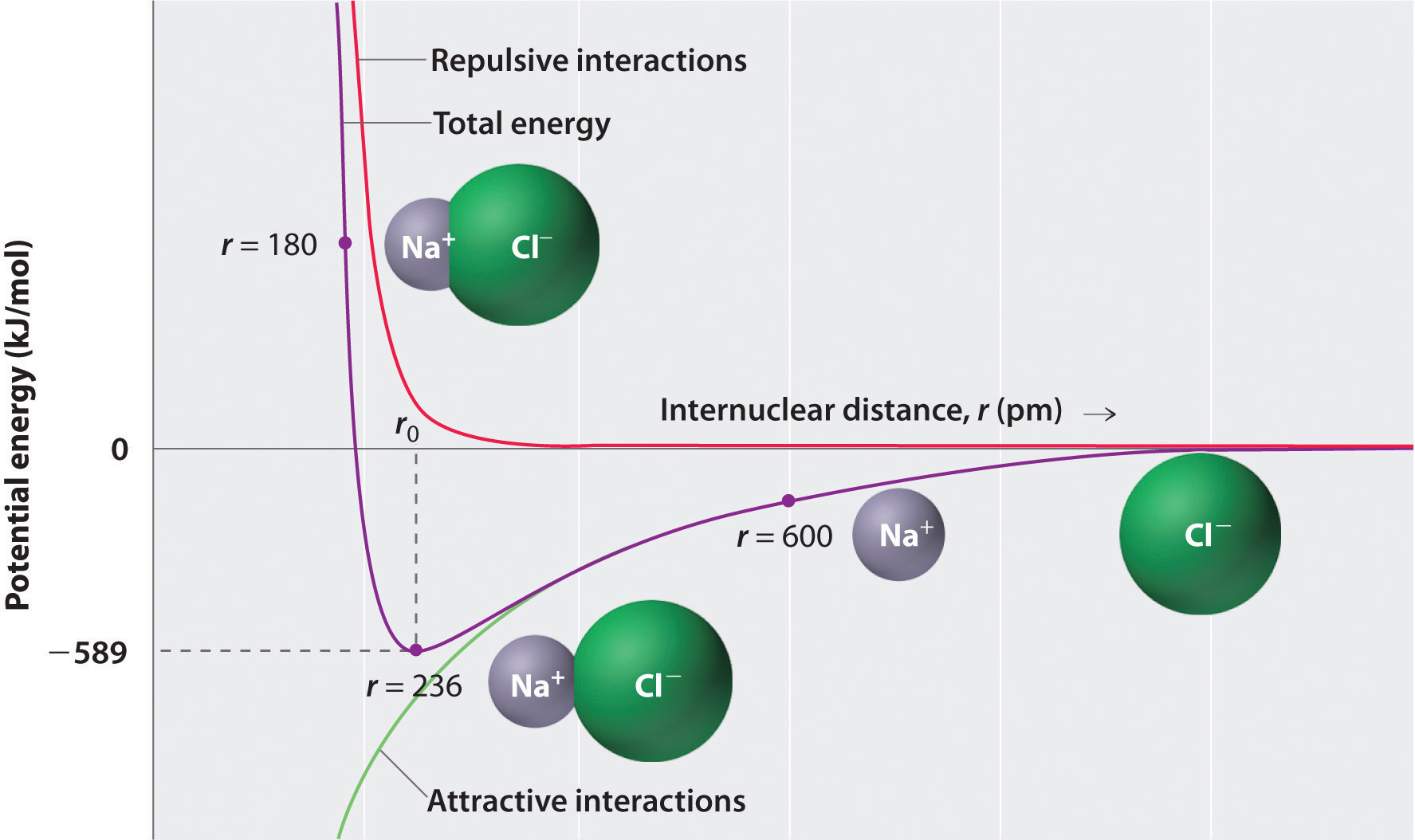
Vurder energien som frigjøres når en gassformig \(Na^+\) ion og en gassformig \(Cl^-\) ion bringes sammen fra r = ∞ til r = r0. Gitt at den observerte gassfaseinternukleære avstanden er 236 pm, er energiendringen forbundet med dannelsen av et ionpar fra en \(Na^+_{(g)}\) ion og a \(Cl^-_{(g)}\) ion som følger:

\ &= (2,31 \ganger {10^ {- 28}}\rm{J}\cdot \cancel{m} ) \venstre( \dfrac{( + 1)( – 1)}{236\; \avbryt{pm} \ ganger 10^ {- 12} \avbryt{m/pm}} \høyre) \\ &= – 9.79 \ ganger 10^ {- 19}\; J / ion\; par \label{Eq2} \ end{align*}\]

den negative verdien indikerer at energi frigjøres. Vår konvensjon er at hvis en kjemisk prosess gir energi til omverdenen, er energiendringen negativ. Hvis det krever energi, er energiendringen positiv. For å beregne energiendringen i dannelsen Av en mol nacl-par, må vi multiplisere energien per ionpar med Avogadros nummer:

\

dette er energien som frigjøres når 1 mol gassformige ionpar dannes, ikke når 1 mol positive og negative ioner kondenserer for å danne et krystallinsk gitter. På grunn av langtrekkende interaksjoner i gitterstrukturen, svarer denne energien ikke direkte til gitterenergien til det krystallinske faste stoffet. Den store negative verdien indikerer imidlertid at å bringe positive og negative ioner sammen er energisk meget gunstig, enten et ionpar eller et krystallinsk gitter dannes.

vi oppsummerer de viktige punktene om ionisk binding:

• ved r0 er ionene mer stabile (har lavere potensiell energi) enn de er i en uendelig internukleær avstand. Når motsatt ladede ioner bringes sammen fra r = ∞ til r = r0, senkes energien i systemet (energi frigjøres).
• på grunn av den lave potensielle energien ved r0, må energi legges til systemet for å skille ionene. Mengden energi som trengs er obligasjonsenergien.
• energien i systemet når et minimum ved en bestemt internukleær avstand (bindingsavstanden).