Rational Exponents
Rational Exponents
Learning Objective(s)
· Convert radicals to expressions with rational exponents.
· Convert expressions with rational exponents to their radical equivalent.
· Use the laws of exponents to simplify expressions with rational exponents.
· Use rational exponents to simplify radical expressions.
はじめに
平方根は、ほとんどの場合、このようなラジカル記号を使用して書かれています。![]()
![]()
![]() と書くことができます。数を有理数の指数に上げることは想像できませんか?
と書くことができます。数を有理数の指数に上げることは想像できませんか?
それらは慣れるのが難しいかもしれませんが、有理数指数は実際にいくつかの問題を単純化するのに役立ちます。 有理数(分数)指数とラジカルの関係を調べてみましょう。
有理数指数を使用してラジカル式を書き換える
ラジカルと分数指数は、同じことを表現する別の方法です。 あなたはすでに、平方根が半分の累乗の指数として表現される方法を見てきました。
|
Radical Form |
Exponent Form |
Integer |
|
|
|
4 |
|
|
|
5 |
|
|
|
10 |
Let’s look at some more examples, but this time with cube roots. 覚えておいて、数を立方体にすると、それは3の累乗になります。 これらの例では、有理指数の分母は数3であることに注意してください。
|
Radical Form |
Exponent Form |
Integer |
|
|
|
2 |
|
|
|
5 |
|
|
|
10 |
These examples help us model a relationship between radicals and 有理数指数:すなわち、数値のn番目の根は、![]()
![]() のいずれかとして書くことができます。
のいずれかとして書くことができます。
|
Radical Form |
Exponent Form |
|
|
|
|
|
|
|
|
|
|
… |
… |
|
|
|
When faced with an 有理数指数を含む式は、基数を使用して書き換えることができます。 上の表では、有理指数の分母が根の指数をどのように決定するかに注目してください。 したがって、![]()
![]()
![]()
![]()
![]() 。
。
|
Example |
||
|
Problem |
Write |
|
|
|
The radical form |
|
|
Answer |
|
|
|
Example |
|||||||
|
Problem |
Express |
||||||
|
|
小数の指数を基数として式を書き直します。 分数の分母が根、この場合は立方根を決定します。p>
|
||||||
|
回答 |
|
||||||
グループ化記号が使用されていない限り、指数はすぐに左にある数量のみを参照することに注意してください。 以下の例は、一つの重要な違いを持つ前の例と非常によく似ています—括弧はありません! 何が起こるか見てください。
|
Example |
||
|
Problem |
Express |
|
|
|
Rewrite the expression with the fractional exponent as a radical. 分数の分母が根、この場合は立方根を決定します。 指数は、指数のすぐ左にある式の一部のみを参照します。xこの場合は2ではなく、2を参照します。 |
|
|
Answer |
|
|
Rewriting Expressions with Rational Exponents Using Radicals
Just as you can rewrite an expression with a rational exponent as a radical expression, you can express a radical expression using a rational exponent.
|
Example |
||
|
Problem |
Express |
|
|
|
Rewrite the radical using a rational exponent. The root determines the fraction. この場合、根基のインデックスは3なので、有理数指数は 4は基数の外側にあるため、グループ化シンボルには含まれず、指数はそれを参照しません。 |
|
|
Answer |
|
|
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the expression with the fractional exponent as a radical. |
|
|
6 • x2 |
Find the square root of both the coefficient and the variable. |
|
|
回答 |
|
|
分子以外の有理数指数
上記の例の小数指数の分子はすべて1でした。 以下に示すように、1以外の分子を持つ小数部の指数を使用して根を表すことができます。 このテーブル内の任意のパターンに気づきますか?
|
Radical |
Exponent |
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
… |
|
|
|
分数指数を使用してラジカルを書き換えると、ラジカンドが発生するべき乗が分子になり、根が分母になります。
分数指数を書く
![]()
![]() の形式の分数指数を使用して書くことができます。
の形式の分数指数を使用して書くことができます。
![]()
![]()
![]()
![]()
![]() の同等の形式でどこから来ているのかを見ることができます。
の同等の形式でどこから来ているのかを見ることができます。
有理数指数と指数の法則を使用してラジカル式を簡素化
今、いくつかのラジカル式を探索し、それらを簡 単純化する必要がある根本的な式は次のとおりです。![]() 。この式を単純化する1つの方法は、この例では以下に示すように、a3のグループを因数分解して引き出すことです。
。この式を単純化する1つの方法は、この例では以下に示すように、a3のグループを因数分解して引き出すことです。
|
Example |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Problem |
Simplify. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Rewrite by factoring out cubes. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Write each factor under its own radical and simplify. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
回答 |
|
回答 |
の形式の根基を使用して書くことができるという原則を使用します。
Note that rational exponents are subject to all of the same rules as other exponents when they appear in algebraic expressions. 両方の単純化方法は、同じ結果、a2を与えました。 問題の文脈によっては、どちらか一方の方法を使用する方が簡単かもしれませんが、今のところ、”プルアウト”方法を使用する場合よりも有理数指数を使用してこの式をより迅速に単純化することができたことに注意してください。別の例を試してみましょう。
再び、別の方法は、ファクタリングを使用してラジカルの下で簡素化に取り組むことです。 あなたが今解決した例では、次のようになります。
Which of the expressions below is equal to the expression A) B) C) D) ショーより複雑な式
分母を単純化することから始めましょう。
まあ、それはしばらく時間がかかりましたが、あなたはそれをしました。 分数指数、負の指数、および指数の規則について知っていることを適用して、式を単純化しました。 要約 根基は、規約 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
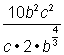
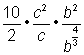
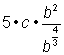
Leave a Reply