Articles

Excelでの線形回帰分析

by admin

チュートリアルでは、回帰分析の基本について説明し、Excelで線形回帰を行ういくつかの異なる方法を示しています。

これを想像してみてください：あなたはたくさんの異なるデータを提供され、あなたの会社の来年の売上数を予測するように求められます。 あなたはおそらく数に影響を与える可能性のある要因の数十、おそらく数百を発見しました。 しかし、どのようにして本当に重要なものを知っていますか？ Excelで回帰分析を実行します。 それはあなたにこれとより多くの質問への答えを与えるでしょう: どの要因が重要で、どの要因を無視できますか？ これらの要因はどのように密接に関連していますか？ そして、あなたは予測についてどのように確実にすることができますか？

  • Excelで回帰分析
  • 分析ToolPakでExcelで線形回帰
  • 線形回帰グラフを描く
  • 数式でExcelで回帰分析

Excelで回帰分析-基本

統計モデリングでは、回帰分析:従属変数（別名基準変数）は、あなたが理解し予測しようとしている主な要因です。

独立変数（別名説明変数、または予測子）は、従属変数に影響を与える可能性のある因子です。

従属変数に影響を与える可能性のある因子です。

従属変数

回帰分析は、独立変数のいずれかが変化したときに従属変数がどのように変化するかを理解するのに役立ち、それらの変数のどれが実際に影響技術的には、回帰分析モデルは、データポイントの分散を見つけるための数学的な方法である二乗和に基づいています。

技術的には、回帰分析モデルは、 モデルの目標は、可能な限り最小の平方和を取得し、データに最も近い線を描画することです。統計では、単純な線形回帰と多重線形回帰を区別します。

統計では、単純な線形回帰と多重線形回帰を区別します。 単純線形回帰は、線形関数を使用して従属変数と1つの独立変数との関係をモデル化します。 従属変数を予測するために2つ以上の説明変数を使用する場合は、多重線形回帰を扱います。 データリレーションシップが直線に従わないために従属変数が非線形関数としてモデル化される場合は、代わりに非線形回帰を使用します。 このチュートリアルでは、単純な線形回帰に焦点を当てます。

例として、過去24ヶ月間の傘の販売数を取り、同じ期間の平均月間降雨量を調べてみましょう。 この情報をチャートにプロットすると、回帰直線は独立変数（降雨）と従属変数（傘売上）の関係を示します。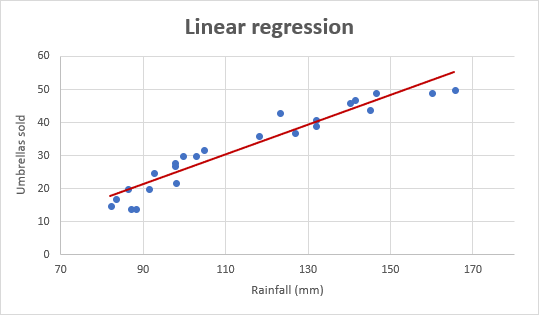

線形回帰方程式

数学的には、線形回帰は次の式で定義されます。

y=bx+a+ε

ここで、

  • xは独立変数です。
  • yは従属変数です。
  • aはY切片で、すべてのx変数が0に等しい場合のyの期待平均値です。 回帰グラフでは、線がY軸を横切る点です。
  • bは回帰直線の傾きで、xが変化したときのyの変化率です。
  • bは回帰直線の傾きで、xが変化したときのyの変化率です。
  • εは、従属変数の実際の値とその予測値との差であるランダム誤差項です。

線形回帰方程式には、実生活では予測変数が完全に正確ではないため、常に誤差項があります。 ただし、Excelを含む一部のプログラムでは、エラー項の計算が舞台裏で行われます。 したがって、Excelでは、最小二乗法を使用して線形回帰を行い、次のような係数aとbを求めます。

y=bx+a

この例では、線形回帰方程式は次の形を取ります。

Umbrellas sold = b * rainfall + a

aとbを見つけるには、いくつかの異なる方法が存在します。Excelで線形回帰分析を実行する主な三つの方法は次のとおりです。:

  • 回帰ツールは、分析ToolPakに含まれています
  • トレンドラインと散布図
  • 線形回帰式

以下では、各メソッドを使用する上での詳細な手順を見つ

分析ToolPakを使用してExcelで線形回帰を行う方法

この例では、分析ToolPakアドインに含まれる特別なツールを使用してExcelで回帰を実行する方法を示

Analysis ToolPakアドインを有効にする

Analysis ToolPakは、Excel2019から2003のすべてのバージョンで使用できますが、既定では有効になっていません。 したがって、手動でオンにする必要があります。 Excelで、ファイルをクリックします。>オプション。

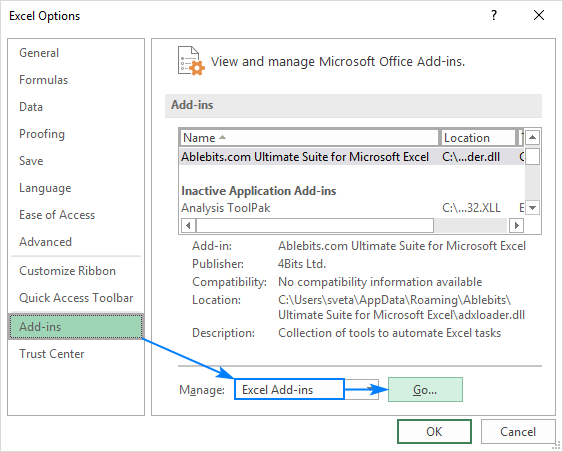
  • Excelオプションダイアログボックスで、左側のサイドバーのアドインを選択し、管理ボックスでExcelアドインが選択されていることを確認し、移動をクリ
  • アドインダイアログボックスで、分析Toolpakをオフにチェックし、OKをクリックします。

    • これにより、Excelリボンのデータタブにデータ分析ツールが追加されます。この例では、Excelで単純な線形回帰を行います。 私たちが持っているのは、独立変数（予測子）である列Bの過去24ヶ月の平均月間降雨量と、従属変数である列Cの傘の販売数のリストです。 もちろん、販売に影響を与える可能性のある他の多くの要因がありますが、今のところ、これらの二つの変数にのみ焦点を当てています。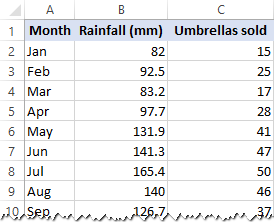

    分析Toolpak addedを有効にして、Excelで回帰分析を実行するには、次の手順を実行します。

    1. データタブの分析グループで、データ分析ボタンをクリックします。
    2. 回帰を選択し、OKをクリックします。
    3. 回帰ダイアログボックスで、次の設定を行います。
      • 従属変数である入力Y範囲を選択します。 私たちの場合、それは傘の販売（C1：C25）です。
      • 入力X範囲、つまり独立変数を選択します。 この例では、月平均降雨量（B1：B25）です。

      重回帰モデルを構築する場合は、独立変数が異なる隣接する2つ以上の列を選択します。XとYの範囲の上部にヘッダーがある場合は、ラベルボックスをオンにします。

    4. お好みの出力オプション、私たちの場合は新しいワークシートを選択します。
    5. 必要に応じて、残差チェックボックスを選択して、予測値と実際値の差を取得します。
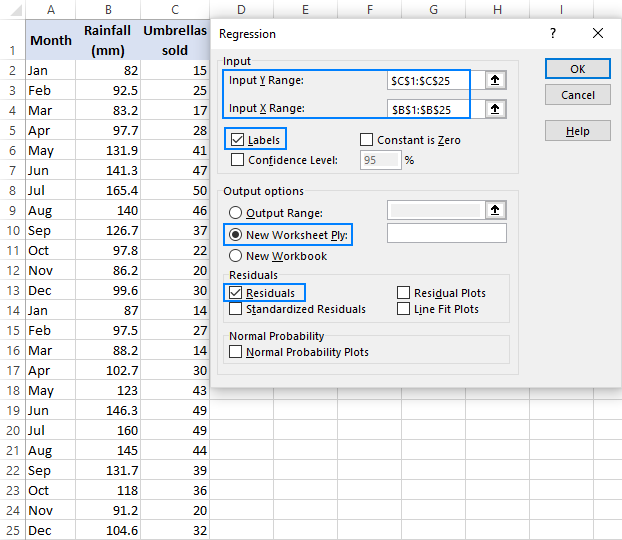
    6. OKをクリックし、Excelで作成された回帰分析出力を観察します。

    回帰分析出力の解釈

    先ほど見たように、すべての計算が自動的に事前に行われるため、Excelで回帰を実行するのは簡単です。 結果の解釈は、各番号の背後にあるものを知る必要があるため、少しトリッキーです。 以下に、回帰分析の出力の4つの主要な部分の内訳を示します。

    回帰分析出力:要約出力

    この部分では、計算された線形回帰方程式がソースデータにどれだけ適合するかを説明します。

    ここでは、情報の各部分が意味するものです：

    複数のR.これは、二つの変数間の線形関係の強さを測定する相関係数です。 相関係数は-1と1の間の任意の値にすることができ、その絶対値は関係の強さを示します。 絶対値が大きいほど、関係が強くなります。

    • 1は強い正の関係を意味します
    • -1は強い負の関係を意味します
    • 0は全く関係がないことを意味します

    R Square。 これは、適合度の指標として使用される決定係数です。 これは、回帰直線上に落ちるどのように多くのポイントを示しています。 R2の値は、総二乗和から計算され、より正確には、元のデータの平均からの偏差の二乗の合計です。この例では、r2は0.91（2桁に四捨五入）であり、これは妖精の良いことです。 これは、私たちの値の91％が回帰分析モデルに適合していることを意味します。 言い換えると、従属変数（y値）の91％は独立変数（x値）によって説明されます。 一般的に、95％以上のR二乗は良好な適合と考えられています。

    調整されたRの正方形。 これは、モデル内の独立変数の数に合わせて調整されたr平方です。 重回帰分析には、R squareの代わりにこの値を使用する必要があります。標準エラー。

    標準エラー。 これは、回帰分析の精度を示す別の適合度尺度であり、数が小さいほど、回帰方程式についてより確実になる可能性があります。 R2はモデルによって説明される従属変数の分散の割合を表しますが、標準誤差は、データポイントが回帰線から落ちる平均距離を示す絶対尺度です。

    観測。 これは単にモデル内の観測値の数です。

    回帰分析出力：ANOVA

    出力の第二の部分は、分散分析（ANOVA）です：

    基本的に、それはあなたの回帰モデル内の変動のレベルに関す

  • SSは平方和です。 残差SSが合計SSと比較して小さいほど、モデルはデータに適合しやすくなります。
  • MSは平均二乗です。
  • Fは、f統計量、または帰無仮説のF検定です。 これは、モデルの全体的な有意性をテストするために使用されます。
  • Significance FはFのP値です。

    • Anova部分は、Excelでの単純な線形回帰分析にはほとんど使用されませんが、最後のコンポーネントをよく見てくださ 有意性F値は、結果の信頼性（統計的に有意）を示します。 有意性Fが0.05（5％）未満の場合、モデルは問題ありません。 それが0.05より大きい場合は、おそらく別の独立変数を選択する方が良いでしょう。

    回帰分析出力:係数

    このセクションでは、分析のコンポーネントに関する具体的な情報を提供します。

    このセクションで最も有用なコンポーネントは係数です。 それはあなたがExcelで線形回帰方程式を構築することができます：

    y=bx+a

    yは販売された傘の数であり、xは月平均降雨量である私たちのデータセッ:

    Y=0.45*x-19.074

    たとえば、平均月間降雨量が82mmの場合、傘の売上は約17.8になります。

    0.45*82-19.074=17.8

    同様の方法で、指定した他の月間降雨量(x変数)で販売される傘の数を調べることができます。

    回帰分析の出力：残差

    あなたは82ミリメートルの毎月の降雨量に対応する販売傘の推定数と実際の数を比較すると、あなたはこれらの数がわずかに異なっていることがわかります：

    • 推定：17。8（上で計算）
    • 実際：15（ソースデータの行2）

    違いはなぜですか？ 独立変数は従属変数の完全な予測子ではないためです。 また、残差は、実際の値が予測値からどれくらい離れているかを理解するのに役立ちます。

    Excelで線形回帰グラフを作成する方法

    二つの変数間の関係をすばやく視覚化する必要がある場合は、線形回帰グラフを描きます。 それは非常に簡単です！ 次の方法があります。

    1. ヘッダーを含むデータを含む2つの列を選択します。

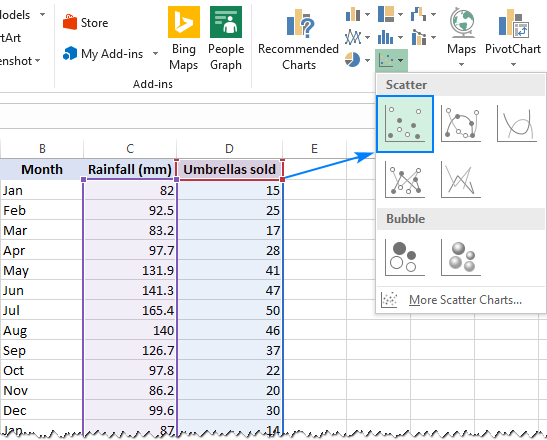
      これにより、ワークシートに散布図が挿入されます。

    2. 次に、最小二乗回帰線を描画する必要があります。 それを行うには、任意の点を右クリックし、コンテキストメニューからトレンドラインを追加…を選択します。
    3. 右ペインで、線形トレンドライン形状を選択し、必要に応じて、チャート上の式の表示をチェックして回帰式を取得します。

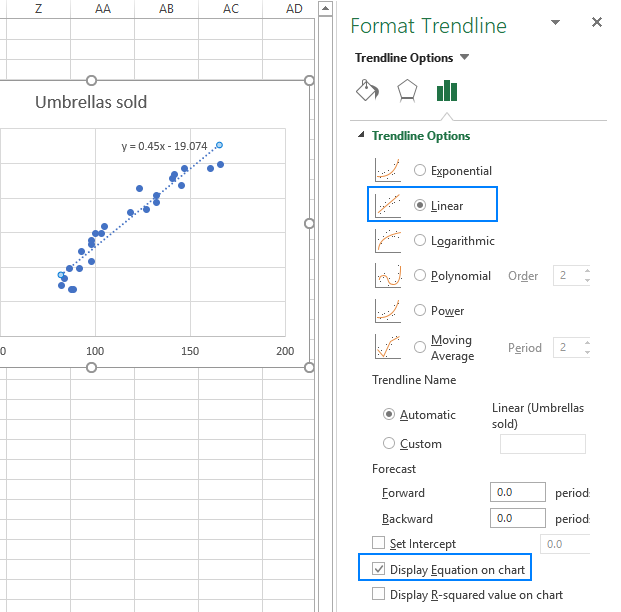
      お気づきのように、Excelが作成した回帰式は、係数出力に基づいて作成した線形回帰式と同じです。

    4. 塗りつぶし&行タブに切り替えて、好みに合わせて行をカスタマイズします。 たとえば、別の線の色を選択し、破線の代わりに実線を使用することができます（ダッシュタイプボックスで実線を選択します）。

    この時点で、チャートはすでにまともな回帰グラフのように見えます。

    まだ、いくつかの改善をしたいことがあります。

    • 数式を適当な場所にドラッグします。
    • 軸のタイトルを追加します（チャート要素ボタン>軸のタイトル）。
    • この例のように、データポイントが水平軸または垂直軸の中央から始まる場合は、余分な空白を取り除くことができます。 次のヒントでは、これを行う方法を説明します。空白を減らすためにグラフ軸を拡大縮小します。

      そして、これは私たちの改善された回帰グラフがどのように見えるかです：

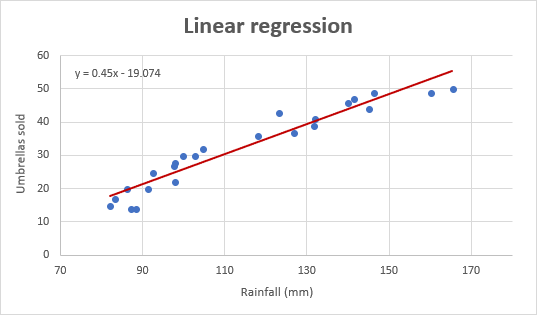      重要な注意！ 回帰グラフでは、独立変数は常にX軸上にあり、従属変数はY軸上にある必要があります。 グラフが逆の順序でプロットされている場合は、ワークシートの列を交換してから、グラフを新たに描画します。 ソースデータの再配置が許可されていない場合は、グラフ内でX軸とY軸を直接切り替えることができます。数式を使用してExcelで回帰を行う方法

      Microsoft Excelには、LINEST、SLOPE、INTERCPET、CORRELなどの線形回帰分析を行うのに役立ついくつかの統計関数があります。

      LINEST関数は、最小二乗回帰法を使用して、変数間の関係を最もよく説明し、その行を記述する配列を返す直線を計算します。 このチュートリアルでは、関数の構文の詳細な説明を見つけることができます。 ここでは、サンプルデータセットの式を作成しましょう。

      =LINEST(C2:C25, B2:B25)

      LINEST関数は値の配列を返すため、配列式として入力する必要があります。 同じ行の2つの隣接するセルE2を選択します:F2この場合、数式を入力し、Ctrl+Shift+Enterを押して完了します。

      式は、すでにおなじみの線形回帰方程式のb係数（E1）とa定数（F1）を返します。

      y = bx + a

      ワークシートで配列式を使用しない場合は、正規式でaとbを個別に計算することができます。

      Get y切片（a）：

      =INTERCEPT(C2:C25, B2:B25)

      傾き（b）を取得します:

      =SLOPE(C2:C25, B2:B25)

      さらに、二つの変数が互いにどのように強く関連しているかを示す相関係数（回帰分析要約出力の倍数R）を見つけることができます。

      =CORREL(B2:B25,C2:C25)

      次のスクリーンショットは、これらすべてのExcel回帰式が動作していることを示しています。
      =CORREL(B2:B25,C2:C25)

      次のスクリーンショットは、これらのExcel回帰式を示しています。

      ヒント。 回帰分析の追加の統計情報を取得する場合は、次の例に示すように、statsパラメーターをTRUEに設定したLINEST関数を使用します。これがExcelで線形回帰を行う方法です。 とはいえ、Microsoft Excelは統計プログラムではないことに注意してください。 専門レベルで回帰分析を実行する必要がある場合は、XLSTAT、RegressItなどのターゲットソフトウェアを使用することをお勧めします。

      利用可能なダウンロード:

      このチュートリアルで説明する線形回帰式やその他のテクニックを詳しく見るには、サンプル回帰分析In ExcelブックP>

      • 例でExcelでソルバーを使用する方法
      • Excelで複利を計算する方法
      • ExcelでCAGR（複合年間成長率）を計算する方法