Articles

Closed system

by admin

in classical mechanicsEdit

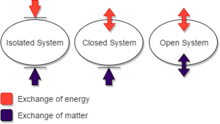
非相対論的古典力学では、閉じたシステムは、その周囲と物質を交換せず、その源がシステムの外部にある正味の力の影響を受けない物理システムである。 古典力学における閉システムは、熱力学における孤立したシステムと同等であろう。 閉じたシステムは、特定の問題や実験の結果に影響を与える要因を制限するために使用されることがよくあります。

熱力学における

主な記事: 熱力学システム
エネルギーと物質を交換する際の孤立した、閉じた、およびオープンシステムの特性。熱力学では、閉じたシステムは（熱や仕事として）エネルギーを交換することができますが、問題ではありません。surroundings.An 孤立したシステムは、熱、仕事、または物質を周囲と交換することはできませんが、オープンシステムはエネルギーと物質を交換することができます。 （用語の定義のこのスキームは、いくつかの目的のために便利ですが、均一に使用されていません。 特に、いくつかの作家は、”孤立したシステム”がここで使用されている”閉じたシステム”を使用します。)

一つのタイプの粒子（原子または分子）のみを持つ単純なシステムの場合、閉じたシステムは一定の数の粒子になります。 しかし、化学反応を受けているシステムのために、反応プロセスによって生成され、破壊されている分子のすべての種類があるかもしれません。 この場合、系が閉じているという事実は、それがどのような分子の一部であっても、各元素原子の総数が保存されていることを示すことによって表 数学的には:

\sum_{{j=1}}^{m}a_{{ij}}N_{j}=b_{i}

ここで、n j{\displaystyle N_{j}}

n_{j}

はj型分子の数であり、a i j{\displaystyle a_{ij}}

a_{ij}

は要素i{\displaystyle i}

iは要素i{\displaystyle i}

iは要素i{\displaystyle i}

iは要素i{\displaystyle i}

iは要素i{\displaystyle i}

iDIV>

分子j{\displaystyle J}

J

およびb i{\displaystyle B_{i}}

B_{i}

は分子j{\displaystyle J}

J

系内の元素i{\displaystyle i}

i

の原子の総数は、系が閉じているので一定のままである。 システム内の異なる要素ごとにそのような方程式が1つあります。

熱力学では、複雑な熱力学的問題を解決するために閉じた系が重要です。 これは、実験や問題の結果を変更する可能性のあるいくつかの外部要因を排除することを可能にし、それを簡素化します。 閉システムは、状況を単純化するために熱力学的平衡が必要な状況でも使用することができる。

in quantum physicsEdit

詳細情報：量子場理論

この方程式は、シュレーディンガーの方程式と呼ばれ、孤立したまたは閉じた量子系、すなわち定義上、情報（すなわちエネルギーおよび/または物質）を別の系と交換しない系の挙動を記述する。 したがって、孤立したシステムが時間tにおいてある純粋な状態|π(t)≤Hにある場合、Hはシステムのヒルベルト空間を表し、この状態の時間発展（2つの連続した測定の間）である。{\displaystyle I\hbar{\frac{\partial}{\partial t}}\psi\Left(\mathbf{r},t\right)={\hat{h}}\Psi\Left(\mathbf{r},t\right)\,\!}\Psi\Left(\mathbf{r},t\right)={\hat{h}}\Psi\Left(\mathbf{r},t\right)={\hat{h}}\Psi\Left(\mathbf{r},t\right)={\hat{h}}\Psi\Left(\mathbf{r},t\right)={\hat{h}}\Psi\Left(\mathbf{r},{\displaystyle i\hbar{\frac{\partial}{\partial t}}\Psi\left(\mathbf{r},t\right)={\hat{H}}\Psi\left(\mathbf{r},t\right)\,\!}