beanz Magazine
ウィキペディアのMerian-Erben(1652)による地図
今月の数学パズルは、スイスの数学者で物理学者であるLeonhard Eulerによって最初に解決された1735年にさかのぼります。パズルはケーニヒスベルクの七つの橋と呼ばれています。
パズルはケーニヒスベルクの七つの橋と呼ばれています。 それは実際の都市に基づいています,その後、プロイセンで,今ロシアのカリーニングラード. 市は二つの島の間にある川で分かれており、さらに下流には川が再び市を分割しています。
この問題は一見単純です。
この問題は単純です。
: オイラーの時代には、2つの島と町の下流の部分を結ぶための7つの橋があります(またはありました)。 オイラーは、人が町のすべての部分に触れるために一度だけ7つの橋のそれぞれを渡って歩くことができるかどうか疑問に思いました。 同じ場所での開始と終了は要件ではありませんでした。
ここでは、自分で問題を解決しようとするために使用できるマップです。
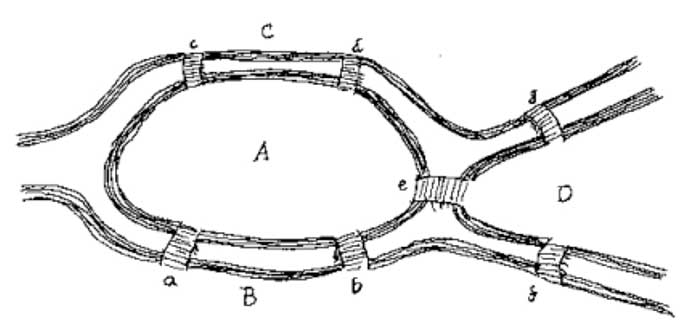
この問題を解決するためには、どちらが重要だと思いますか: 橋の数や各橋の場所?答え:橋の数。
オイラーは、各橋の上を一度歩いてケーニヒスベルクの各部分に移動したい場合は、橋の数が偶数でなければならないことを証明しました。 このソリューションでは、各ブリッジを端点、数学的には頂点、および各ブリッジ間の接続(頂点)として表示します。 オイラーは、偶数の橋だけが橋を二度渡ることなく町のすべての部分に触れることができるという正しい結果をもたらしたことを実現しました。
オイラーは数学を使って、7つの橋を一度だけ横断してケーニヒスベルクのすべての部分を訪れることは不可能であることを証明しました。
そうすることで、彼は空間と交差する空間をどのように定義することができるか、そしてそれらの特性についての一連の発見と洞察を動かしました。 オイラーの解の詳細な説明は、この記事の下のWikipediaリンクにあります。たとえば、メビウスのストリップを見たことがあるなら、トポロジーの例を見たことがあります。 トポロジーは、空間と物事が互いにどのように接続するか、そして空間の連続性と境界に関係しています。 トポロジーはまた、空間の性質がどのように変化するかを研究し、空間が拡大または縮小されたときに変化しない。
コンピューティングでは、トポロジーは、データが任意のシステム内で流れることができるネットワーク(パス)と、データのセットが互いにどのように関連 ケーニヒスベルクの七つの橋はまた、オイラーの問題の七つの橋のような制限のセットを与えられた最も効率的なルートを見つけようとする時には旅行セールスマン問題と呼ばれる別の一般的な計算問題に似ています。
非数学者(おそらくあなた、間違いなく私)は、電車やバスに乗るたびに旅行セールスマンの問題を経験します。 旅行セールスマンの問題は、指定された距離の都市のペア間を移動する最も効率的な方法を考え出しています。 有限のルートに沿って移動する希少なリソース(列車、バス)を管理することは、コンピュータがより速く、より効率的であるため、計算を解決するための完 しかし、まず、問題を述べ、数学で解を定義するためにオイラーや他の人が必要です。 私達はそれから計算をするために私達のコンピュータをプログラムする。
トポロジーはまた、物事のグループは、他のグループだけでなく、ユニークな要素と共通の要素を識別するためにセットにソートすることができますどのように、集合論を扱っています。 ベン図は、セットの良い例です。 プログラミングでは、データをさまざまな方法でソートする必要があります。 どのソート方法が状況に最も適しているかは、集合論によって決定することができます。
オイラーの時代から七つの橋はどうなったのですか?
2つの橋は取り壊され、1つの高速道路に置き換えられました。 残りの3つの橋のうち、1つは1935年に再建され、他の2つはオイラーが知っていたようにそのまま残っています。 そして、もちろん、ケーニヒスベルク、プロイセンはカリーニングラード、ロシアにその名前を変更しました。
Leave a Reply