イオン結合形成のエネルギー学

イオン結合は、正と負に帯電したイオンが静電力によって一緒に保持されているときに形成される。 イオンの単一のペア、1つの陽イオンと1つの陰イオンを考えてみましょう。 彼らの魅力の力はどれくらい強いでしょうか？ クーロンの法則によれば、2つの荷電粒子間の静電引力のエネルギー（\(E\)）は、電荷の大きさに比例し、粒子間の核間距離（\(r\)）に反比例する。:比例定数kは2.31×10-28J·mに等しい。kのこの値には、各イオンに対する単一の電子（1.6022×10-19C）の電荷が含まれる。 この式は、定数に組み込まれたクーロン(C)で表される各イオンの電荷を使用して記述することもできます。 この場合、比例定数kは8.999×109J·m/C2に等しくなります。 与えられた例では、Q1=+1（1.6022×10-19C）およびQ2=-1（1.6022×10-19C）である。 Q1とQ2が反対の符号を持つ場合（例えばNaClのように、Q1はNa+に対して+1であり、Q2はCl−に対して-1である）、Eは負であり、反対に帯電したイオンが無限の距離から一緒になって孤立したイオン対を形成するときにエネルギーが放出されることを意味する。

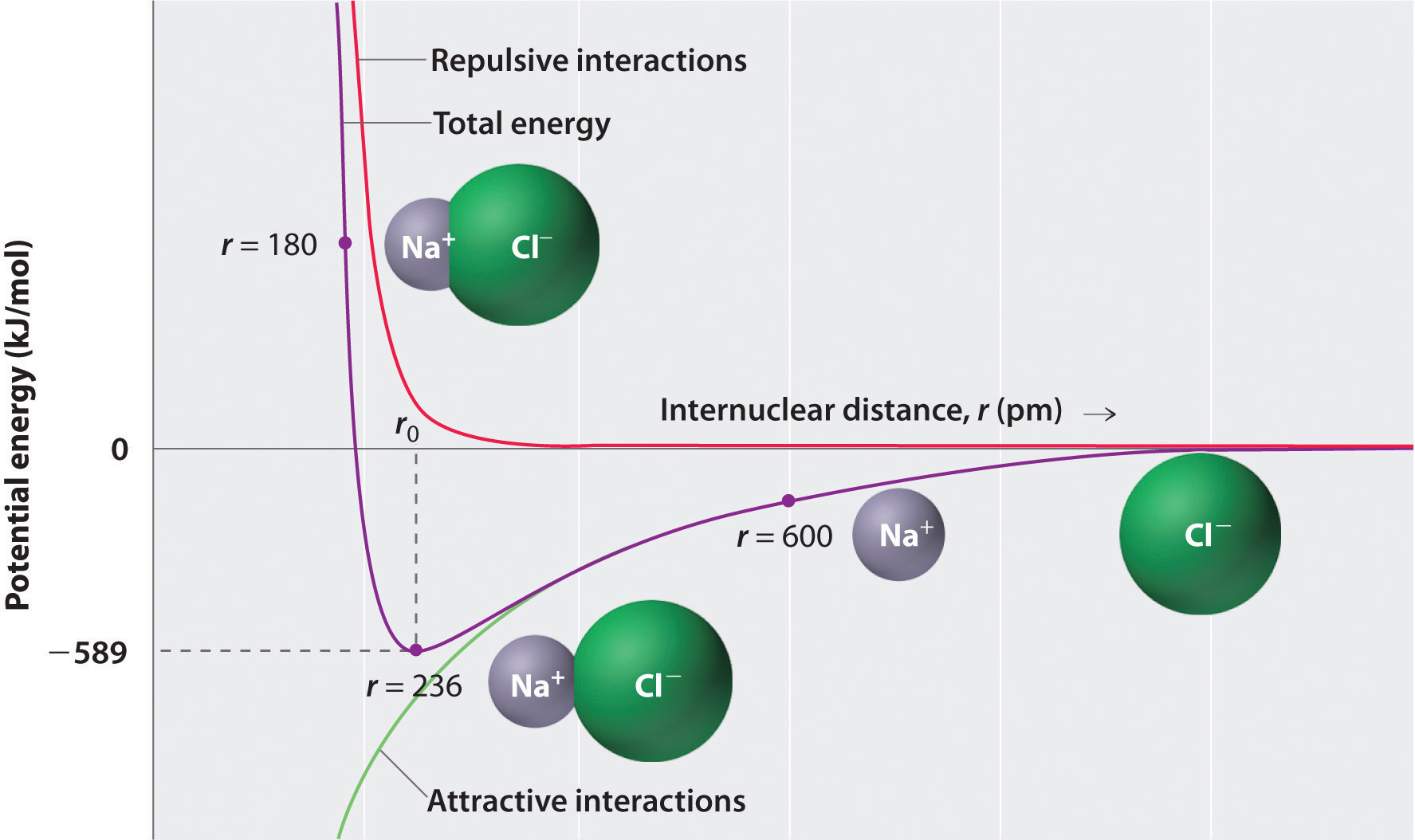
エネルギーは常に結合が形成されるときに放出され、それに対応して、それは常に結合を破るためにエネルギーを必要とします。図\(\PageIndex{1}\)の下半分の緑色の曲線で示されているように、最大エネルギーは、r=0で、イオンが互いに無限に近いときに放出されます。 しかし、イオンは空間を占有し、正の核が電子に囲まれた構造を持っているため、無限に接近することはできません。 非常に短い距離では、隣接するイオン上の電子間の反発電子–電子相互作用は、図\(\PageIndex{1}\)の上半分の赤い曲線で示されるように、反対の電荷を持つイオン間の引力相互作用よりも強くなる。 系の全エネルギーは引力相互作用と反発相互作用の間のバランスである。 図\(\PageIndex{1}\)の紫色の曲線は、システムの総エネルギーがr0で最小に達し、静電反発と引力が正確にバランスされていることを示しています。 この距離は、実験的に測定された結合距離と同じである。p>

\&=(2.31\times{10^{-28}}\rm{J}\cdot\cancel{m})\left(\dfrac{( + 1)( – 1)}{236\; \{pm}\回10^{-12}\キャンセル{m/pm}}\右）\\&=-9。10^{-19}\;J/ion\;pair\label{Eq2}end{align*}\]負の値はエネルギーが放出されていることを示します。 私たちの慣習は、化学プロセスが外の世界にエネルギーを提供する場合、エネルギー変化は負であるということです。 それがエネルギーを必要とするならば、エネルギー変化は肯定的です。 NaCl対のモルの形成におけるエネルギー変化を計算するには、イオン対あたりのエネルギーにアボガドロの数を掛ける必要があります:

\

これは、1molの正イオンと負イオンが凝縮して結晶格子を形成するときではなく、1molの気体イオン対が形成されたときに放出されるエネル 格子構造における長距離相互作用のために、このエネルギーは結晶性固体の格子エネルギーに直接対応しない。 しかし、大きな負の値は、イオン対または結晶格子が形成されているかどうかにかかわらず、正と負のイオンを一緒にもたらすことがエネルギー的に非常に有利であることを示している。

イオン結合についての重要なポイントを要約します:

• r0では、イオンは無限核間距離にあるよりも安定しています（ポテンシャルエネルギーが低い）。 逆に帯電したイオンがr=πからr=r0に一緒になると、系のエネルギーが低下する（エネルギーが放出される）。
• r0のポテンシャルエネルギーが低いため、イオンを分離するためにエネルギーをシステムに追加する必要があります。 必要なエネルギーの量は結合エネルギーです。
• システムのエネルギーは、特定の核間距離（結合距離）で最小に達する。

例\(\PageIndex{2}\): LiF

分離されたイオンから1molのガス状Li+F−イオン対が形成されたときに放出されるエネルギー量を計算する。 気相中で観測された核間距離は156pmである。

与えられた：陽イオンと陰イオン、量、および核間距離

求められた：ガス状イオン対の形成から放出されるエネルギー

戦略：

式\(\ref{Eq1B}\)に適切な値を代入して、単一のイオン対の形成で放出されるエネルギーを得、この値にアボガドロの数を掛けてモル当たり放出されるエネルギーを得る。

解決策

解決策:式\(\ref{Eq1B}\)にLi+F−の値を挿入すると（Q1=+1、Q2=−1、r=156pm）、li+F-イオンの単一のペアの形成に関連するエネルギーは、

\&=\left(2.31\times10^{-28}J J\cancel{m}\right)=\left(2.31\times10^{-28}J J\cancel{m}\right)=\left(2.31\times10^{-28}J J\cancel{m}\right)=\left(2.31\times10^{-28}j J\cancel{m}\right)=\left(2.31\times10^{-28}j J\cancel{m}\right)=\left(10^{-28}j⋅)\left(\dfrac{\text})\left(\dfrac{\text}){(+1)(-1)}}{156\; 10^{−12}\キャンセル{m/pm}}\右）\\&=-1.48\回10^{-18}\端{整列*}\]

その後、Li+Fイオン対のモル当たりに放出されるエネルギーは

\&-891 \;Li+とF−はNa+とCl-よりも小さいため（セクション7.3を参照）、LiFの核間距離はNaClよりも短い。 その結果、式\(\ref{Eq1B}\)によれば、1molのガス状のLi+F−イオン対が形成されたとき（-891kJ/mol）、1molのガス状のNa+Cl−イオン対が形成されたとき（-589kJ/mol）よりもはるかに多くのエネルギーが放出される。1molの気体\(\ce{MgO}\)イオン対が分離されたイオンから形成されたときに放出されるエネルギーの量を計算する。\(\ce{MgO}\)イオン対が形成されたときに放出されるエネルギーの量を計算する。\(\ce{MgO}\)イオン対が形成されたときに放出されるエネルギーの量を計算する。\(\ce{mgo}\)イオン対が形成されたときに放出されるエネルギーの量を計算する。 気相中の核間距離は175pmである。

答え

-3180kJ/mol=-3.18×103kJ/mol