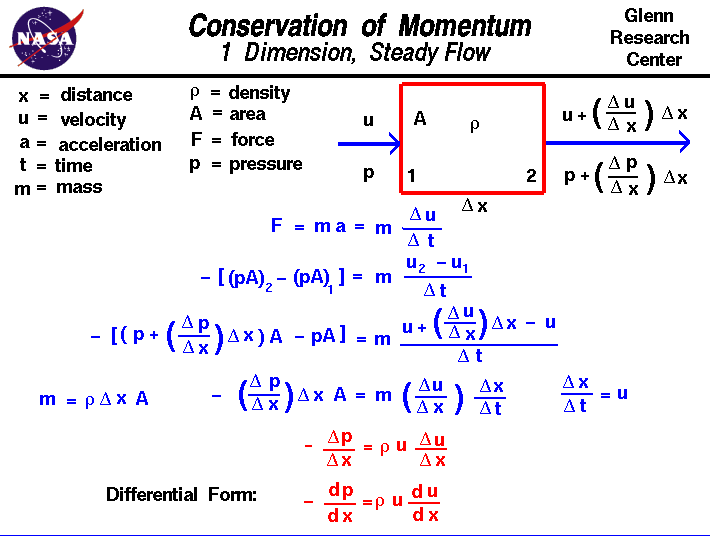
流れの性質を持つ領域を通るガスの流れを考えてみましょう一方向にのみ変化し、これを”x”と呼びます。 ガスはある速度uで第1ステーションに入り、ある圧力pandは速度と圧力の異なる値で第2ステーションに出る。 簡単にするために、密度rはドメイン内で一定のままであり、ガスが流れる領域Aも一定のままであると仮定する。 駅1と駅2の位置は、del xと呼ばれる距離によって分離されています（Deltaはスライド上の小さな三角形であり、ギリシャ文字”d”です。 数学者はしばしばこの記号を使用して量の変化または変化。 Web印刷フォントはサポートしていませんギリシャ文字なので、単に”del”と呼びます。）距離による変化は勾配と呼ばれ、速度と呼ばれる時間による変化との混同を避けるために勾配と呼ばれます。速度勾配は、del u/del xによって示され、距離における速度変化の変化である。 したがって、ステーション2では、速度は速度1に勾配を加えた距離を加えたもので与えられます。p>

同様の式は、出口に圧力を与えます:

ニュートンの運動状態の第二法則力Fは時間に対する運動量の変化に等しい。 一定のmassmを持つオブジェクトの場合、これは質量倍の加速度に減少しますa.An 加速度は、時間の変化に伴う速度の変化（del u/del t）です。 次に：

この問題の力は圧力勾配から来ます。 圧力は単位面積当たりの力であるため、流体ドメイン上の正味の力は、圧力にexitの面積を引いた圧力に入り口の面積を掛けたものです。

この式の先頭のマイナス記号は、ガスが高圧の領域から低圧の領域に移動するために使用されます。 速度と圧力の式を代入する：

単純化:

(del x/del t)はベロシティであり、質量は密度r倍の体積（面積倍del x）であることに注意してください。

(del x/del t)は体積であり、質量は密度r倍の体積（面積倍del x）であることに注意してください。

iv id=”

-(del p/del x)*del x*a=r*del x*a*(del u/del x)*u

-(del p/del x)=r*u*(del u/del x)

-(del p/del x)=r*u*(del u/del x)

-(del p/del x)=r*u*(del u/del x)

-(del p/del x)=r*u*(del u/del x)

-(del p/del x)=r*u*(del u/del x)

-(del u/del x)

-(del u/del x)

/p>

-dp/dx=r*u*du/dx