複素数：はじめに（ページ1の3）

セクション：はじめに、複合体を持つ演算、二次式

今まで、あなたは負の数の平方根を取ることはできません。 それはあなたがそれらを二乗した後に負の数を持っていなかったからです（それであなたは平方根を取って「後方に行く」ことができませんでした）。 あなたがそれを二乗した後、すべての数は正でした。 だから、あなたは否定的な平方根をうまく平方根できず、賢明なものを思いつくことを期待することができませんでした。しかし、今、あなたは負の数の平方根を取ることができますが、それはそれを行うために新しい数を使用することを含みます。 この新しい番号が発明されました（発見されましたか？）は、宗教改革の時期に設立された日本の宗教法人。 当時、特定の方程式を解くことに関わる計算を容易にする以外に、この新しい数には”現実世界”の使用が見つかるとは誰も信じていなかったので、新しい数は便宜のために発明されたふりをした数であると見なされた。（しかし、あなたがそれについて考えるとき、すべての数字の発明ではありませんか？ それは数字が木に成長するようなものではありません！ 彼らは私たちの頭の中に住んでいます。 私たちはそれらをすべて作りました！ 私たちがすでに持っているもので大丈夫である限り、新しいものを発明しないのはなぜですか？ulこれを行うことができます：

しかし、これは意味がありません！ あなたはすでに1に二乗する2つの数字、すなわち-1と+1を持っています。 そして、私はすでに-1に平方します。 だから私も1に二乗するのは合理的ではありません。 これは重要な詳細を指摘しています: 想像力を扱うとき、あなたは何かを得る（平方根の中のネガを扱う能力）が、あなたは何かを失う（平方根を扱うときに持っていた柔軟性と便利なルールの 特に、あなたは常に最初のi-部分を行う必要があります！

• sqrt(-9)を単純化します。 Copyright©Elizabeth Stapel2000-2011All Rights Reserved

（警告：第三の”等号”記号を通過するステップは、”“ではありません。 私はラジカルの外にあります。)

• sqrt(-25)を単純化します。

• sqrt(-18)を単純化します。

• 単純化–sqrt(-6)。 あなたの計算では、x2はちょうどx2であるが、i2は–1であるという事実を除いて、xと同じようにiを扱います。
  • 2i+3iを単純化します。

  2i+3i=(2+3)i=(2+3)i=(2+3)i=(2+3)i=(2+3)i=(2+3)i=(2+3)i=(2+3)i=(2+3)i=(2+3)i=(2+3)i=(2+3)i=(2+3)i=(2+3)i=(2+3)i=(2+3)i=(2+3)i=(2+3)i=(2+3)i=(2+3)i=(2+3)i=(2+3)i=(2+3)i=(2+3)i=(2+3)5i

  • 16i-5iを簡素化します。16i–5i=(16–5)i=11i
  • 乗算して単純化します(3i)(4i)。(3i)(4i)=(3·4)(i·i)=(12)(i2)

  (3i)(4i)=(3*4)(i*i)=(12)(i2)

) = (12)(-1) = -12

• 乗算と単純化(i)(2i)(–3i).

(i)(2i)(–3i)=(2·–3)(i·i·i)=(-6)(i2·i)

=(-6)(-1·i)=(-6)(-i)=6i

この最後の問題に注意してください。 その中には、i2=-1であるため、が表示されます。 続けて、我々は得る:

このべき乗、符号、1、およびiのパターンはサイクルです。

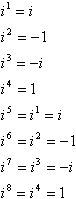
言い換えれば、iの任意の高電力を計算するには、最も近い倍数を取ることによって、より低い電力に変換することができます。これは指数よりも大きくなく、指数からこの倍数を減算します。 たとえば、テストに関する一般的なトリックの質問は、”I99を簡素化する”という線に沿ったものです。iを九十から九回掛けて時間がなくなり、教師は教員ラウンジであなたの費用で良い笑いを得るでしょう。 ここでは、ショートカットがどのように動作するかです:

i99=i96+3=i(4×24)+3=i3=–i

つまり、i99=i3,あなただけのi96をオフに垂れすることがで （Ninety-sixは4の倍数なので、i96は1だけです。）言い換えれば、指数を4で除算し（長除算を使用）、答えを破棄し、残りのみを使用することができます。 これはあなたが気にする指数の部分をあなたに与えるでしょう。 ここにいくつかの例があります：

• I17を簡素化します。I17=i16+1=i4·4+1=i1=i

• I120を単純化します。

i120=i4·30=i4·30+0=i0=1

• I64,002を単純化します。

i64,002 = i64,000 + 2 = i4 · 16,000 + 2 = i2 = –1

Top | 1 | 2 | 3 | Return to Index Next >>