一つの変数の線形不等式のグラフは数直線です。 <>には開円を使用し、≤と≥には閉じた円を使用します。p>

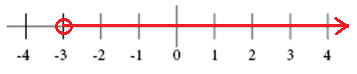
xのグラフ>-3

x≤2のグラフ

同じ解を持つ不等式は等価と呼ばれます。 不平等の性質があり、平等の性質がありました。 以下のすべての性質は、πとπを含む不等式にも当てはまります。

不等式の加算プロパティは、不等式の各辺に同じ数を追加すると、同等の不等式が生成されることを言います

if if\:x>y,\:then\:x+z>y+z$ $

if if\:X<y,\:次に\: x+z<y+z$ $

不等式の減算プロパティは、不等式の両側から同じ数を減算すると同等の不等式が得られることを示しています。

if if\:x>y,\:then\:x-z>y-z$ $

if if\:X<y,\:then\:x-z<y,\:then\:x-z<y,\:then\:x-z<y,\:then\:x-z<y,\:then\:x-z<不等式の乗算プロパティは、正の数の不等式の両側での乗算が等価な不等式を生成することを示しています。p>

if if\：x>y\：および\: z>0のとき、\:そ\:xz>yz$$

$$場合\:x<y\：\:z>0のとき、\:そ\: xz<yz$$

この掛け算の各側面での格差が負の数は発生しないと同等の不平等をなくしても逆の方向の格差シンボル

$$場合\:x>y\：\:z<0の\:そ\:xz<yz$$

$$場合\:x<y\：\: z<0,\:then\:xz>yz$ $

同じことが不等式の除算プロパティにも当てはまります。

正の数を持つ不等式の両側の除算は、同等の不等式を生成します。frac x>y\：および\：z>0、\：then\：\frac{x}{z}>\frac{y}{z}if

if if\：X>y\:と\:z>0,\:then\: inequality\frac{x}{z}<\frac{y}{z}negative

負の数の不等式の両側で除算すると、不等式記号が逆になると等価な不等式が生成されます。frac x>y\：と\：z<0、\：then\：\frac{x}{z}<\frac{y}{z}if

if if\：X>y\：と\：z<0、\：then\：\frac{x}{z}<\frac{y}{z}if

if if\：X<\frac{y}{z}if0,\:then\:\frac{x}{z}>\frac{y}{z}multi

マルチステップ方程式を解くときと同じように、マルチステップ不等式を解きます。 一度に一つのことを取ることは、好ましくは、定数から変数を単離することによって開始します。 多段階の不等式を解くときは、負の数で乗算または除算するときに不等式記号を逆にすることを忘れないことが重要です。inequality-2\left（x+3\right）<10inequalityを解く

inequality-2\left（x+3\right）<10inequality

inequality-2\left（x+3\right）<10inequality