Articles

簡単な順列と組み合わせ

by admin

私はいつも”順列”と”組み合わせ”を混乱させてきました—どれがどれですか？

覚えやすい方法は次のとおりです：順列は複雑に聞こえますよね？ そして、それはあります。 順列では、すべての小さな詳細が重要です。 Alice,Bob and CharlieはCharlie,Bob and Aliceとは異なります（ここに友達の名前を挿入してください）。一方、組み合わせは非常に簡単です。

詳細は関係ありません。 Alice,Bob and CharlieはCharlie,Bob and Aliceと同じです。

順列はリスト（順序の問題）のためのものであり、組み合わせはグループのためのものです（順序は問題ではありません）。あなたが知っている、”組み合わせロック”は本当に”順列ロック”と呼ばれるべきです。

あなたが知っている、”組み合わせロック”は本当に”順列ロック”と呼ばれるべきです。 あなたが問題に数字を入れた順序。

簡単な順列と組み合わせ

真の”コンビネーションロック”は、10-17-23と23-17-10の両方を正しいものとして受け入れます。P>

順列：毛むくじゃらの詳細

順列、または何かを行うすべての可能な方法から始めましょう。 私たちはfancy-pantsという用語”順列”を使用しているので、各アイテムの順序を含むすべての最後の詳細を気にします。 私たちは8人を持っているとしましょう：

1: Alice2: Bob3: Charlie4: David5: Eve6: Frank7: George8: Horatio

八人の出場者の中で1位、2位、3位の賞を授与する方法はいくつありますか？ (Gold/Silver/Bronze)

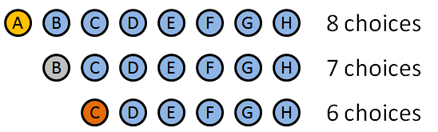
permuation example medals

これらのメダルを配る順序が重要なので、順列を使用します。 ここでは、それが分解する方法です：

  • ゴールドメダル：8選択肢：A B C D E F G H（私は名前が文字と一致させた巧妙な方法、えっ？). Aが金を獲得したとしましょう。
  • 銀メダル：7選択肢：B C D E F G H.のは、bが銀を獲得したとしましょう。
  • 銅メダル：6個の選択肢：C D E F G H.のは、言ってみましょう…Cは銅メダルを獲得します。私たちは勝つために特定の人を選んだが、詳細は問題ではない：私たちは最初に8つの選択肢を持っていた、その後7、その後6。 オプションの合計数は次のとおりでした$8 * 7 * 6 = 336$.詳細を見てみましょう。

    私たちは3人のうち8人を注文しなければならなかった。 これを行うために、私たちはすべてのオプション（8）から始め、メダルがなくなるまで一度に1つずつ（7、6）を奪いました。私たちは階乗が知っている

    :

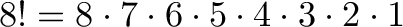
    \displaystyle{8! =8\cdot7\cdot6\cdot5\cdot4\cdot3\cdot2\cdot1}

    残念ながら、それはあまりにも多くを行います！ また$8 * 7 * 6$. 階乗を5で「停止」するにはどうすればよいですか？

    これは順列がクールになる場所です：私たちがどのように取り除きたいかに注意してください$5 * 4 * 3 * 2 * 1$. これの別の名前は何ですか？ 5階乗！

    だから、私たちは8を行う場合！/5! 私たちは得る：

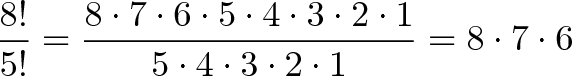
    \displaystyle{\frac{8！}{5! div frac{8\cdot7\cdot6\cdot5\cdot4\cdot3\cdot2\cdot1}{5\cdot4\cdot3\cdot2\cdot1}=8\cdot7\cdot6}

    なぜ5という数字を使ったのですか？ 3つのメダルを8つ選んだ後に残っていたので。 したがって、これを書くより良い方法は次のようになります。

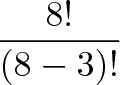
    \displaystyle{\frac{8！}{(8-3)!}}

    ここで8！/(8-3)! “8の最初の3つの数字を使用してください！”. 合計n個のアイテムがあり、特定の順序でkを選択したい場合は、次のようになります。

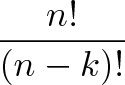
    \displaystyle{\frac{n！}{(n-k)!あなたはn個のアイテムを持っていて、k個のアイテムを注文する方法の数を見つけたいと思っています。

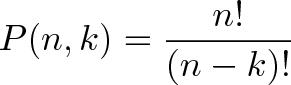
    \displaystyle{P（n、k）=\frac{n！}{(n-k)!}}

    組み合わせ、Ho！

    順序は関係ない あなたはそれを混ぜることができ、それは同じように見えます。 私はcheapskateであり、別々の金、銀、銅メダルを買う余裕がないとしましょう。 実際には、私は空のブリキ缶を買う余裕ができます。

    3つの缶を8人にいくつの方法で与えることができますか？まあ、この場合、私たちが人を選ぶ順序は問題ではありません。

    私がAlice、Bob、そしてCharlieに缶を与えると、Charlie、Alice、そしてBobに与えるのと同じです。 いずれにしても、彼らは同様に失望しています。

    これは興味深い点を提起します—ここにはいくつかの冗長性があります。 アリス-ボブ-チャーリー=チャーリー-ボブ-アリス しばらくの間、3人を並べ替える方法をいくつか見てみましょう。最初の人には3つの選択肢があり、2番目には2つ、最後には1つしかありません。

    まあ、私たちは最初の人に3つの選択肢を持っています。

    だから我々は持っている$3 * 2 * 1▲3人を再配置する方法。ちょっと待って…これは少し順列のように見えています！ 私をだましたのね!確かに私はしました。

    確かに私はしました。 あなたがN人を持っていて、それらのすべてにいくつの手配があるかを知りたいのであれば、それはちょうどN階乗またはNです！

    だから、私たちは離れて与えるために3つのブリキ缶を持っている場合、3があります！ または私達が選ぶあらゆる選択のための6つの変化。 私たちが持っている組み合わせの数を把握したい場合は、すべての順列を作成し、すべての冗長性で除算します。 私たちの場合、（上から）336の順列が得られ、各順列の6つの冗長性で除算され、336/6=56になります。P>

    一般式は

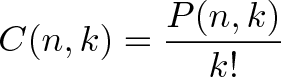
    \displaystyle{C（n、k）=\frac{P（n、k）}{k！これは、

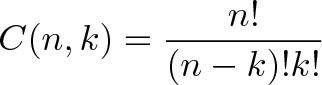    \displaystyle{C（n、k）=\frac{n！}{(n-k)!k!P>C(n,k)は次のように書かれることがあります。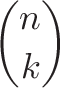

    \displaystyle{\binom{n}{k}}

    これは二項係数です。

    いくつかの例

    ここでは、順列からの組み合わせ（順序は関係ありません）のいくつかの例です（順序は関係ありません）（順序は関係ありません）。

    • 組み合わせ：10人のグループから3人のチームを選ぶ。 $C（10,3）=10！/(7! * 3!) = 10 * 9 * 8 / (3 * 2 * 1) = 120$.

      順列：10のグループから社長、副社長、ウォーターボーイを選ぶ。 $P（10,3）=10！/7! = 10 * 9 * 8 = 720$.

    • 組み合わせ：10のメニューから3つのデザートを選択します。 C（10,3）=120。

      順列：10のメニューから、順番に、あなたの3お気に入りのデザートを一覧表示します。 P（10,3）=720。

    数式を暗記しないで、なぜ動作するのかを理解してください。 組み合わせは順列よりも簡単に聞こえますが、それらはそうです。 あなたは順列よりも少ない組み合わせを持っています。

    このシリーズの他の投稿

    1. 簡単な順列と組み合わせ
    2. 組み合わせと順列を使用してグリッドを移動
    3. 乗算を使用して組み合わせを理解する方法
    4. なぜ組み合わせを乗算するのですか？