等価分数を理解する

等価分数は、全体の同じ部分を表します

たとえば、パイを真ん中に正確にカットした場合、同じサイズのパイが二つになり、一枚はパイの半分と同じになります。

そして、別のパイ（同じサイズ）が4つの等しい部分に切断された場合、そのパイの2つの部分は、1/2がしたのと同じ量のパイしたがって、1/2は2/4と同等（または同等）であると言うことができます。同等の分数を混同させてはいけません！

あなたを混乱させてはいけません！

上の四つの円を見てみましょう。1つの「1/2」、2つの「1/4」、および4つの「1/8」が、円のためにオレンジ色に着色された同じ量の領域を占めることがわかりますか？まあ、それはオレンジ色で着色された各領域が同等の分数または等しい量であることを意味します。 したがって、1/2は2/4に等しく、1/2も4/8に等しいと言うことができます。 そして、はいバッタ、2/4は4/8の同等の分数ですtoo.As あなたはすでに知っている、私たちはルールについてナットです。 それでは、2つの分数が同等か等しいかどうかを確認するためのルールを見てみましょう。 同等の分数のルールは説明するのが少し難しいかもしれませんが、そこにハングアップすると、ほんの少しで物事をクリアします。

ここにルールがあります

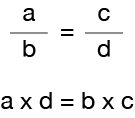
このルールは、最初の分数の分子（a）と他の分数の分母（d）の積が等しい場合にのみ、二つの分数最初の分数の分母（b）と他の分数の分子（c）。製品は単にあなたが乗算することを意味します。

それは一口のように聞こえるので、数字でそれを試してみましょう…

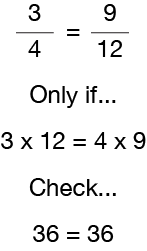
ルールをテスト

今、あなたが”冷たい”それを持っていることを確認するために、同等の分数のルールに数字を差し込んでみましょう。 3/4は、最初の分数の分子（3）と他の分数の分母（12）の積が、最初の分数の分母（4）と他の分数の分子（9）の積に等しい場合にのみ、9/12と同等（等しい）です。 したがって、3×12=36および4×9=36であるため、3/4は9/12に相当することがわかります。 同等の分数をチェックする方法を見る簡単な方法は、1つの分数の分子を他の分数の分母で倍数にすることを意味する「交差乗算」と呼ばれることを その後、逆に同じことを行います。 次に、2つの答えを比較して、それらが等しいかどうかを確認します。 それらが等しい場合、2つの分数は同等の分数です。この例でわかるように、1/2は2/3の同等の分数ではありません。

さて、分数が同等ではない数字で1つをやりましょう…

この例でわかるように、1/2は2/3の同等の分数ではありません。交差乗算法を使用することを覚えている場合は、同等の分数を検証するのに問題はありません。

交差乗算法を使用する場合は、同等の分数を検

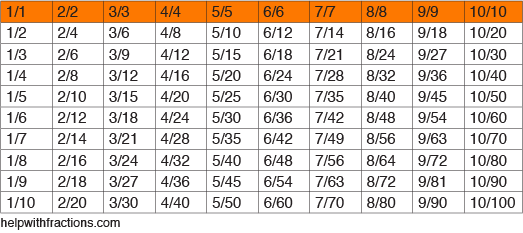
以下の表は、いくつかの一般的な分数とその同等のものを示しています。 テーブルを左から右に読むだけです。 それがあなたに示しているのは、”1″に等しい分数の異なるバリエーションを掛けた値です。 あなたはそれ自体で割った任意の数が右”1″に等しいことを覚えていますか？p>