By Jason McCormick
准教授、市民&環境工学、ミシガン大学、アナーバー、MI、USA

長方形と正方形の中空構造部（HSS）で作られたモーメント）。 これらの接続に焦点を当てた静的研究の大部分は、Vierendeelトラスシステムを考慮しています。 これらのシステムは、多くの場合、正方形または長方形の垂直ウェブ（分岐）メンバーと接続されている正方形または長方形の上部および下部のコードによ この構成の結果として、コードに網の関係はせん断および軸負荷と共に重要な曲がることを経、一般に典型的なトラスシステムでされるようにピン もともと1896年にArthur Vierendeelによって考案されましたが、Hssが開発されるまで、Vierendeelトラスの可能性が実現され始めました（Korol et al. 1977年）、しかし、それらの使用は、HSS-TO-HSS T-接続間でモーメントを転送する方法の理解を必要とした。

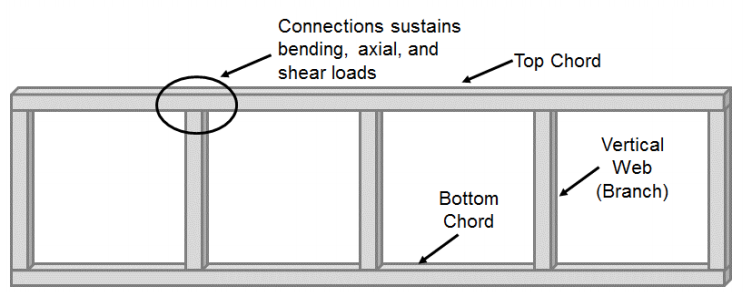
これらの関係の早い調査の多数は枝メンバーの完全な時容 Jubb and Redwood(1966)は、分岐部が弦部（β=1）と等しい幅を有するとき、hss部材の完全なモーメント容量は補強なしで達成できることを示した。 しかし，本研究では，軸方向荷重の存在によるモーメント容量の潜在的な損失は考慮されなかった。 一方、Ｋｏｒｏｌ ｅ ｔ ａ ｌ． (1977)は、弦よりも小さな枝幅を持つ接続は、29の異なる接続テストのシリーズを通じて補強せずに枝の完全なモーメント容量を開発できないことを示した5 一般に，非強化Ｖｉｅｒｅｎｄｅｅｌ型接続の強度と剛性は，弦細長比（Ｂ／ｔ）の増加と枝対弦幅比（β）の減少とともに減少した。 その結果、分岐対弦幅比が1.0であり、弦細長比が低いか、または接続が強化されている場合にのみ、不均等なVierendeelトラス型接続は剛性とみなすことができ

これらの関節の最大モーメントは過度に大きな変形で発生する可能性があるため、軸方向に荷重された正方形および長方形のHSS関節に使用される AISC360-10(Chapter K3)は、静的な面内曲げの下での正方形および長方形のHSS T接続の三つの限界状態を考慮しています：弦壁の塑性化、側壁の局所降伏、および不均一な荷重分布に起因する枝の局所降伏。 弦壁の塑性化は、枝部材の幅が弦の幅（β≤0.85）よりも小さい結果として起こり、曲げモーメントによって生成される張力および圧縮荷重が、より硬い側壁に直接ではなく、弦の比較的柔軟な面を通って伝達される必要がある。 限界状態方程式（AISC360-10方程式K3-6）は、降伏線理論（図2）から導出することができます。

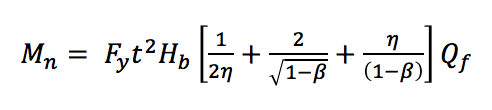
Mnは接続の公称モーメント容量、Fyは弦の指定された最小降伏強度、Hbは枝の全高さ、hは枝の高さを弦の幅で割った荷重長パラメータ（Vierendeelトラスの典型的なように弦と枝部材の間の90°の角度を仮定する）、Qfは弦の幅で割った荷重長パラメータである。コード内の軸方向の圧縮の存在下で関節の容量を低減するためのパラメータ。

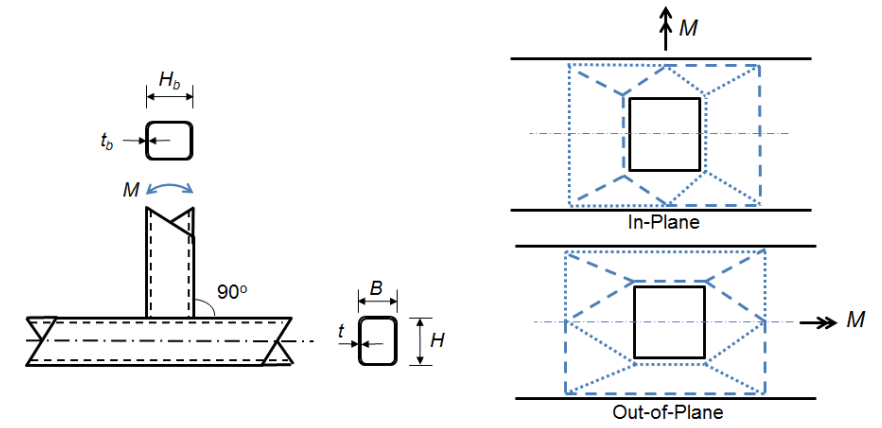
他の二つの限界状態は、分岐部材の幅が和音の幅に等しいか、ほぼ等しい接続に関連付けられている(β>0。85)意味枝メンバーのフランジで開発される張力および圧縮の負荷はコードのより堅いサイドウォールにほとんど直接移ります。 次いで、ｔ接続の側壁局所降伏（ＡＩＳＣ３ ６ ０−１ ０式Ｋ３−７）の限界状態は、その深さよりも大きい部材の端部からの距離で加えられる集中力（ＡＩＳＣ３ ６ ０−１ ０式Ｊ１ ０−２）に対す5fyt(Hb+5t)2
式2

t接続における不均一な負荷分布（AISC360-10式K3-8）による枝の局所的な降伏のために、有効幅アプローチは、ブレースによって適用される公称モーメントを得るためにブレース部材の容量を減らすために使用されます。

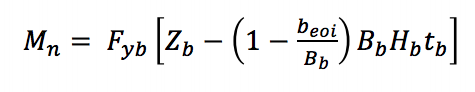
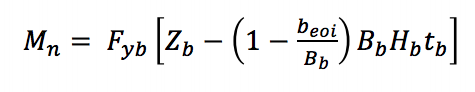
Fybは枝の指定された最小降伏強度、Zbは曲げ軸に関する枝の塑性断面係数、beoiは枝の有効幅、Bbは枝の全幅、tbは枝の設計壁厚です。

平面外曲げの下でVierendeelトラス接続（T接続）の特定の設計モデルをサポートするための実験的証拠が限られているため、平面内曲げの場合と同様の極限状態が使用されている（Packer et al. 2010). 弦歪み破壊の一つの追加の限界状態は，面外モーメントの結果として枝部材によって弦に加えられるトルクから発展する。 このトルクは、弦の菱形の歪みにつながる可能性があります。 面外曲げの公称モーメント方程式は、AISC360-10方程式K3-9、K3-10、K3-11、およびK3-12で見つけることができます。 Ｔ接続の面内曲げおよび面外曲げの両方についての方程式は、国際的に採用されている方程式と同様である（Ｐａｃｋｅｒ ｅ ｔ ａ ｌ． 2010).

上記の設計方程式は、静的荷重下でのVierendeelトラス系を考慮して導出した。 最近の研究（Fadden et al. 2015年）は、管ベースの地震モーメントフレームシステム（中間および特別なモーメントフレーム）で使用するための大きな周期荷重下での正方形および長方形のHSS-HSSモーメント接続の挙動を考慮するために、この作業を進めている。 そのようなシステムは正方形および長方形HSSの優秀な軸、曲がること、およびねじり特性、高強さに重量の比率および建築学上では喜ぶ性質を利用す 高いねじり抵抗はビーム側面固定の減少をより低い地震固まりの高強さに重量の比率の結果がもたらすことができる間、もたらすことができる。 しかしながら、そのような接続は、ビーム部材のプラスチック容量の80％が0.2radのいずれかに維持されるビーム部材の安定したプラスチックヒンジングを （IMF）または0.4rad。 （341-10）。 モーメントフレーム系の現在の耐震設計では，梁部材に非弾性挙動の大部分が発生する必要があることを考えると，梁部材も局所座屈を受ける前に完全な塑性能力に達しなければならない。 Fadden and McCormick(2014a)は、現在のAISC地震規定（AISC341-10）で指定されているものは、主に環状軸方向にロードされたHSS部材の試験に基づいて開発されたため、曲げ下のhssの限界幅-厚さ

この強度と延性の要求を満たすための適切な構成と詳細な要件を決定するために、二つの直接溶接された非強化接続（比類のない、マッチング）と二つの強化接続（プレートと外部ダイヤフラム板を介して）を実験的に試験した。 すべての接続は、HSS10x10x5/8列を使用していました。 直接溶接された接続は、AWS D1.1（2010）で指定されているように、事前に認定されたCJP溶接を利用しました。 比類のない接続のために、ビームはHSS12x8x3/8（β=0。8)コラムの表面のplastificationが心配であるかもしれないことを提案します。 一致させた関係のために、ビームはHSS12x10x3/8(β=1.0)だったサイドウォールに直接移るように負荷がする。 地震時の関係のprequalificationのためのAISCのローディングの議定書は関係に荷を積むのに利用された(AISC341-10)。 接続の挙動は予想通りであり，一致した接続は柱面で変形を示したが，一致した接続は柱側壁に荷重を伝達することができた。 しかし、両方の接続は、溶接部の角のつま先にある柱の母材の破壊のために失敗しました（図3）。 0.4radの回転でこの脆性破壊。 そして0.5rad。 それぞれ、直接溶接された関係が地震適用に適切な行動を提供しないことを確認した。

補強された接続は、その後、列の側壁に張力と圧縮力を伝達し、溶接部にかかる応力集中を最小限に抑えるためのより良いメカニズムを提供するために、ワイドフランジビーム-hssカラム接続によく使用されるプレートと外部ダイヤフラム板を介して考慮して開発されました。 これらの接続のために、ビームはHSS12x8x3/8（β=0.8）メンバーであった。 これらの接続を設計および詳細化するために使用される特定の手順に関する情報は、Ｆａｄｄｅｎ ａｎｄ Ｍｃｃｏｒｍｉｃｋ（２ ０ １ ４ｂ）およびＦａｄｄｅｎ ｅ ｔ ａ ｌ． (2015). 補強されていない接続と同じ荷重下に置かれた接続は、貫通板または外部ダイヤフラム板の端部で柱面から離れて発生するプラスチックヒンジで、より安定した挙動を示しました(図4)。 両方の接続も0.4radに達することができました。 時容量の低下で起因したローカル座屈を経る前の回転の。 しかし、破壊は0.7radの大きな回転レベルでのサイクリングのためにHSSビームのコーナーで開始しました。 一致したダイアフラム板接続と外部ダイアフラム板接続の正規化されたモーメント回転曲線の比較を図5に示します。 全体として、補強された接続は、HSS-TO-HSS地震モーメントフレームシステムの使用の約束を示しましたが、これらの接続を最終的な事前認定に向けて移動す

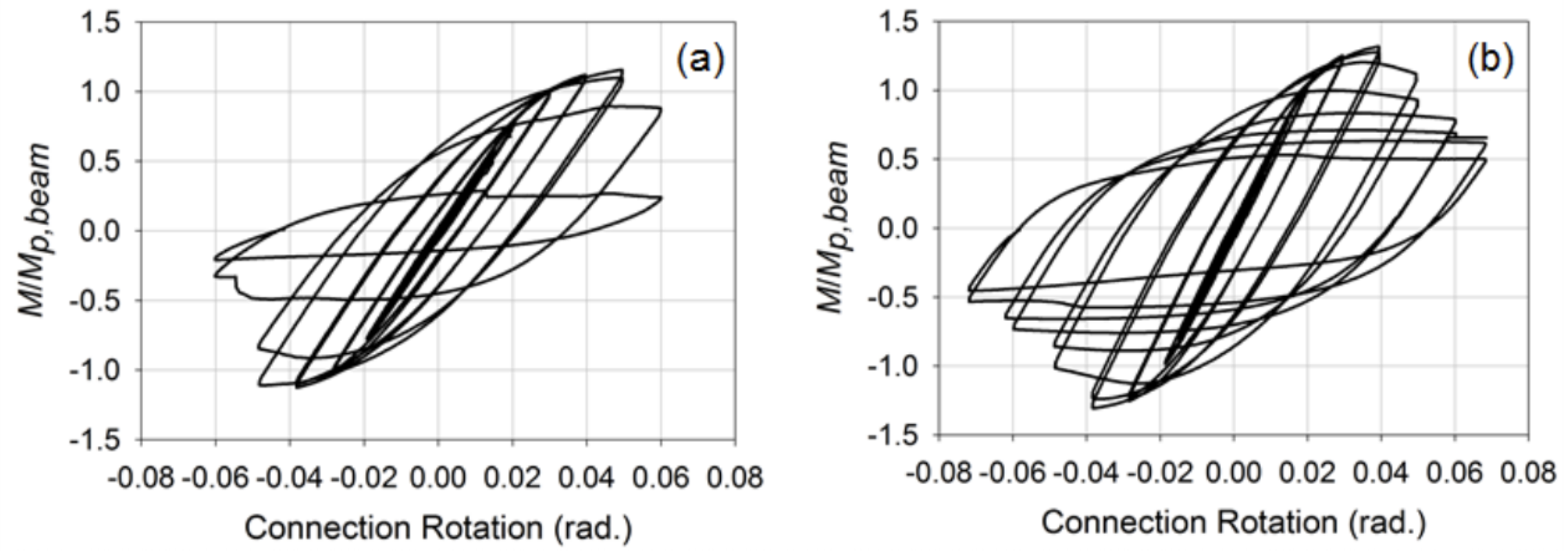
AISCの正規化されたモーメント対接続回転プロット。 (2010). “構造スチールの建物のための地震準備”。 ANSI/AISC341-10. アメリカン-インスティテュート-オブ-スチール-コンストラクション、シカゴ、イリノイ州。

AISC。 (2010). “構造スチールの建物のための指定”。 ANSI/AISC360-10。 アメリカン-インスティテュート-オブ-スチール-コンストラクション、シカゴ、イリノイ州。

AWS。 (2010). “構造溶接コード”。 ANSI/AWS D1.1,American Welding Society,Miami,FL.

Fadden,F. およびＭｃｃｏｒｍｉｃｋ，Ｊ． “中空構造断面の繰返し曲げ挙動の有限要素モデル”。 構造的な鋼鉄研究のジャーナル、94、64-75。

Fadden,F.And McCormick,J.(2014b). “HSS-TO-HSS地震モーメント接続性能と設計”。 構造的な鋼鉄研究のジャーナル、101、373-384。

Fadden,F.,Wei,D.,And McCormick,J.(2015). “地震適用のための溶接されたHSSにHSSの時の関係の循環テスト”。 構造工学のASCEジャーナル,141(2),04014109-1-14.

Jubb,J.E.M.And Redwood,R.G.(1966). “箱セクションへの接合箇所の設計”。 構造エンジニアの機関、工業化された建物および構造エンジニアの会議、構造エンジニアの協会、ロンドン。

Korol,R.M.,El-Zanaty,M.,And Brady,F.J.(1977). “Vierendeelのトラスの正方形の空セクションの不均等な幅の関係”。 土木工学のカナダジャーナル、4、190-201。

Packer,J.A.(1993). “長方形の空セクション間の時の関係”。 構造的な鋼鉄研究のジャーナル、25、63-81。

Packer,J.A.,Wardenier,J.,Zhao,X.-L.,van der Vegte,G.J. そして、Kurobane,Y.(2010)。 設計ガイド3:主に静的なローディングの第2版の下の長方形の空セクション(RHS)の接合箇所のため。 CIDECT、カナダ。

Wardenier,J.(1982). “中空セクションの関節”。 デルフト大学出版社、デルフト、オランダ。

2016年9月

PDFをダウンロード