数学はスプリントよりもマラソンの多くです—それは画期的なまれな瞬間で、長く、遅く、安定した挽くです。 それでも、たまには、私たちはそれらの珍重された”ユーレカ”の瞬間、永遠に科学を変える文字と数字の短い行を得るのです。 ここでは、古代ギリシャ人から現代物理学に、最も有名な方程式のいくつかは、次のとおりです。

これは、すべての幾何学的な柱の中で最も重要な柱の1つです。

これは、すべての幾何学的な柱の中で最も重要な柱の1つです。

これは、: 直角三角形では、斜辺の正方形（直角の反対側）は、他の2つの正方形の合計に等しくなります。 この理論は一般的にギリシャの数学者ピタゴラスに起因していますが、バビロニアの数学者がこの式を理解していたという証拠がいくつかあります。 定理が多くの人々に知られていた可能性も非常に高いですが、彼はそれを証明した最初の人でした。

この定理には多くの証明が与えられています—おそらくあらゆる数学的定理の中で最も多くの証明が与えられています。

それらは幾何学的証明と代数的証明の両方を含む非常に多様であり、いくつかは数千年前にさかのぼります。

複素数

イタリアの数学者Gerolamo Cardanoは、複素数を導入したことが知られている最初の人であり、当時は「架空」 しかし、-1の平方根を表す虚数としての”i”の数学的発展は、人類史上最も重要な数学者で科学者の一人であるレオンハルト-オイラーに帰せられている。

複素数は基本的には存在しない数値ですが、多くの計算には非常に便利です。 それらは実数部（私たちが知っている数字）と虚数部（ここで表されるi）を持つ数字で構成され、物理学、化学、生物学、経済学、電気工学、統計学など、多くの分野で実用的なアプリケーションを持っています。/p>

対数

対数は基本的にべき乗の逆関数です。 同じことを書く別の方法のように見えるかもしれませんが（ある意味ではそうです）、対数には心理学、経済、多くの物理現象（pHや地震の大きさなど）の測定に使用されている無数の実用的な用途があります。対数は1614年にジョン—ネイピアによって公に提唱され、”Mirifici Logarithmorum Canonis Descriptio”（対数のすばらしい規則の記述）というタイトルの本で出版された。 対数の特殊な場合は自然対数—eであり、eは約2.71828182845に等しい非合理的かつ超越的な数である。 実際には、e自体は魅力的な歴史とアプリケーションの印象的な数を持っていますが、それは別の時間のための物語です。

微積分

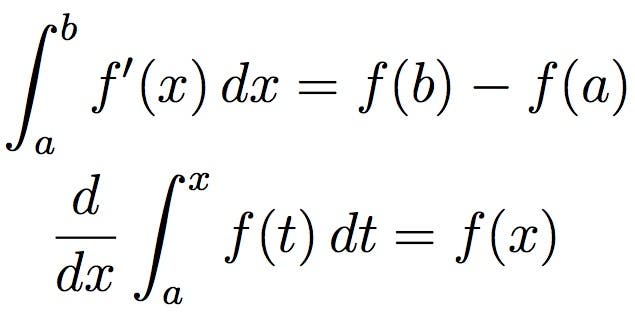
微積分ほど影響力のある数学の分野はほとんどありません。 17世紀にIsaac NewtonとGottfried Wilhelm Leibnizによって開発された微積分は、科学、工学、経済学で広く使用されています。 微積分は、通常、少量、特に無限に少量を扱うことに焦点を当てています。 微積分学を通して、これらは技術的に無限に小さいにもかかわらず、実数として扱うことができます。より簡単な視覚化のために、上に示されている積分は、関数によって定義される曲線の下の面積を測定するものと考えることができます。

重力の法則

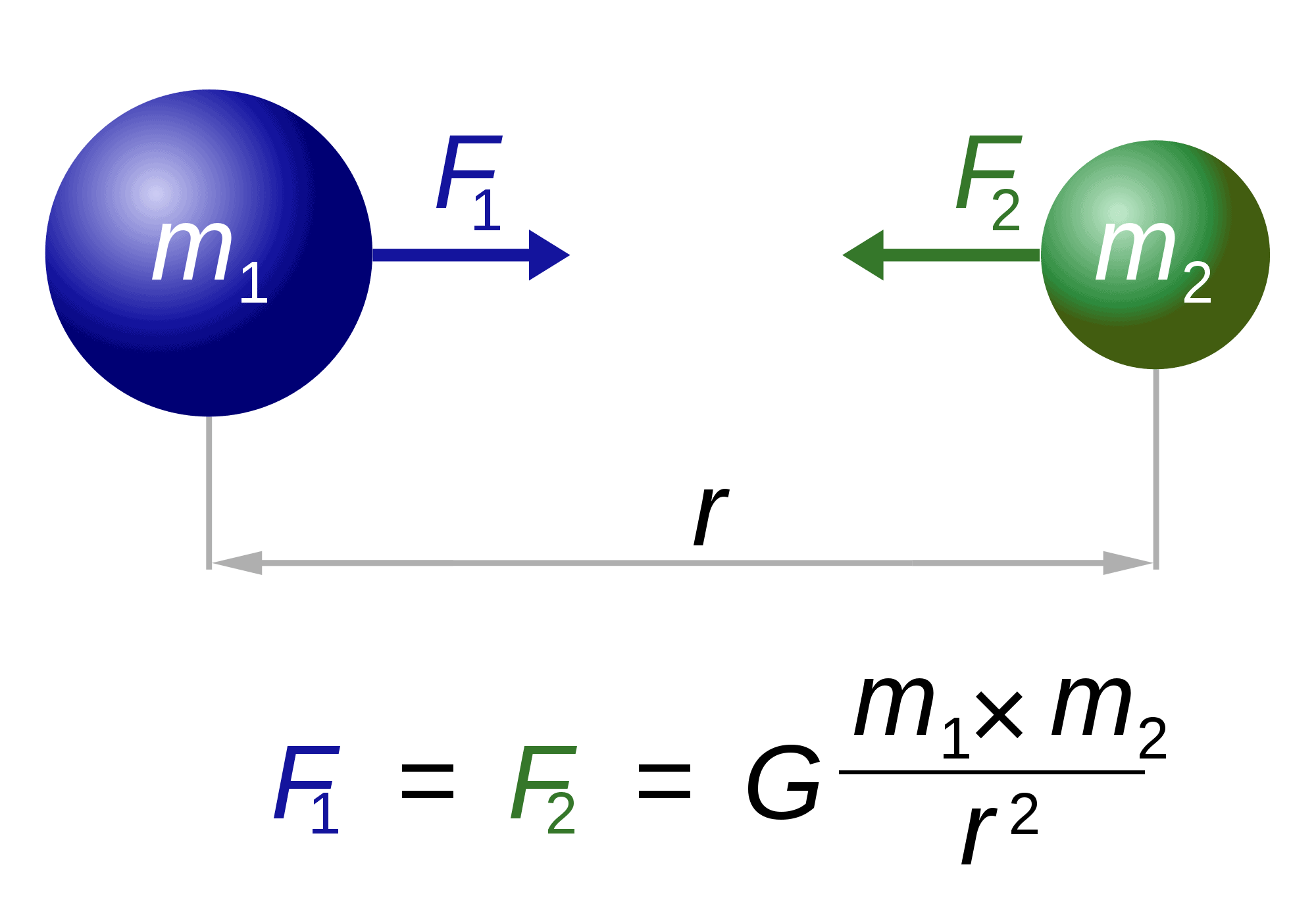
ニュートンといえば、彼はまた、世界で最も有名で壮大な方程式の一つに”責任”があります：重力の法則。

この法則は、基本的に、質量m1とm2の任意の二つの物体が互いに引き付けられる方法を記述しています。 力（F1、F2）は、それらの間の距離（r）の二乗に反比例します。 唯一残っている因子Gは重力定数である。 この定数の性質はとらえどころのないままです。ほぼ200年間、ニュートンの法則は力学の理解の私たちのレベルを定義しました。 20世紀のアインシュタインの仕事は、次のレベルに物事を取った—これら二つの成果は、物理学の世界で最高の台座に塔。一般相対性理論は本質的に重力の幾何学的理論であり、ニュートンの理論を一般化して、空間と時間、または時空の幾何学的性質として重力の統一された記述を提供する。 特に、アインシュタインは、三次元と4次元の時間をマージする”時空”のようなものがあることを示しただけでなく、この時空は重力によって湾曲することができ、曲率は物質や放射線が存在するもののエネルギーと運動量に直接関係していることも示した。

熱力学の第二の法則は、私たちが宇宙で素敵なものを持つことができない理由です。

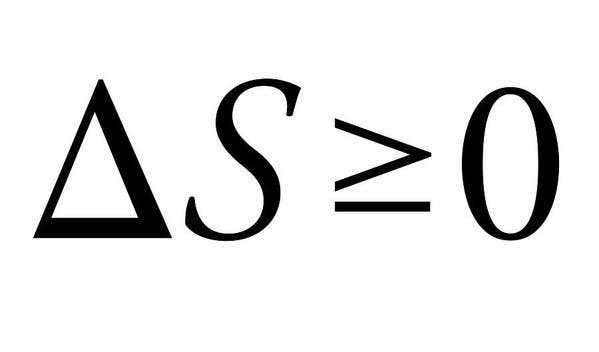
熱力学の第二の法則は、私たちが宇宙で素敵なものを持つことができない理由です。 冗談はさておき、熱力学の4つの法則は、熱力学系を特徴付ける基本的な物理量（温度、エネルギー、エントロピー）を定義します。 第二のものは、特に、そのシンプルさのためにここで際立っていますが、絶対に大規模な意味があります。

この法則は本質的に、相互作用する熱力学系のエントロピーの合計は常に増加しなければならない、または最も一定のままでなければならないと述べている。 エネルギーがある形から別の形に変化したり、物質が動き回ったりすると、閉じたシステムのエントロピー（または無秩序）が増加します。 温度、圧力、密度のすべての違いはしばらくすると平らになる傾向があります

マクスウェルの方程式

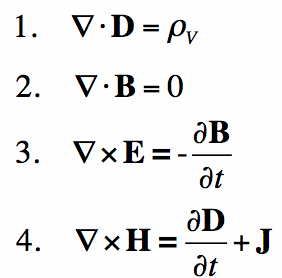
簡単に言えば、マクスウェルの方程式はニュートンの法則が力学にある電磁気学です。 それらは、古典的な電磁気学、古典的な光学、および電気回路の数学的基盤を提供します。 彼らは広くあなたがこれを読んでいる非常にデバイスで使用されています—基本的には、すべての電子デバイス。マクスウェルの法則は、電荷、電流、および磁場の変化によって電場と磁場がどのように生成されるかを記述します。

マクスウェルの法則は、電荷、電流、およ 重要なブレークスルーは、電場と磁場が光の速度で伝播することを実証したことでした。

オイラーの恒等式

最後に、これはおそらく最もエレガントな方程式であり、最高の美しさのものです。

• 0は加算と減算に中立であり、
• 1は乗算と除算に中立である。
• eは乗算と除算に中立である。
• eは乗算と除算に中立である。
• eは乗算と除算に中立である。
• eは乗算と除算に中立である。
• eは乗算と除算に中立である。
• eは乗算と除算に中立である。
• eは乗算と除算に中立である。
• eは乗算と除算に中立である。オイラー数（上記参照）、自然対数の底;
• iは虚数単位（上記参照）; そして、
• πは円周の直径に対する円周の比であるpiです。

これらすべての数を統一する関係を見つけることは息をのむほど短いものではなく、非常にありそうにないようです。 デモは正確には単純ではありませんが、ここで見ることができます。

スタンフォード大学の数学教授キース—デヴリンがこの方程式を説明したのは、”愛の本質を捉えるシェイクスピアのソネットや、肌の深い人間の形の美しさを引き出す絵のように、オイラーの方程式は存在の深みにまで到達する”と言っているだけです。

数学や物理学がシンプルでエレガントな方程式に沸騰することはよくありませんが、そうすると、それは見るべき光景です。