明確な積分
最初に積分の紹介を読んでみたいと思うかもしれません!
統合
|
統合は、領域、ボリューム、中心点および多くの有用なものを見つけるために使用することができます。 しかし、このような関数のグラフの下の領域を見つけるためによく使用されます。 |
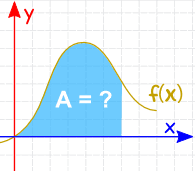 |
|
|
領域は、幅がゼロに近づくスライスを追加することによって見つけることができます。 そして、私たちが答えを得るのに役立つ積分のルールがあります。 |
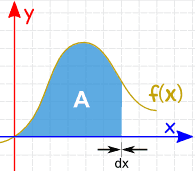 |
表記
“積分”のシンボルは、スタイリッシュな”s”(”合計”のために、スライスを合計する考え)です:
積分シンボルの後、我々は(被積分
そして、dxで終了して、スライスがx方向に移動する(幅がゼロに近づく)ことを意味します。
定積分
定積分には開始値と終了値があります。 aとb(limits、boundsまたはboundariesと呼ばれる)は、次のように”S”の下部と上部に配置されます。
aとb(limits、boundsまたはboundariesと呼ばれる):
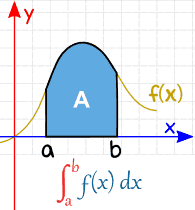 |
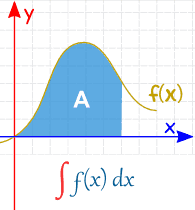 |
|
| Definite Integral (from a to b) |
Indefinite Integral (no specific values) |
We find the Definite Integral by calculating the Indefinite Integral at a, and at b, then subtracting:
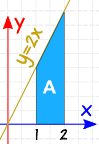
例:2≤1 2x dxとは何ですか
1から2までの定積分を求められています2x dx
最初に不定積分を見つける必要があります。Integration2x dx=x2+C
ここで、1と2でそれを計算します。
- X=1で:∫2x dx=12+C
- x=2で:Subtract2x dx=22+C
- 減算します。
減算します。
減算します。
減算します。
減算します。
減算します。
減算します。
減算します。
減算します。
減算します。
減算します。:
そして、”C”はキャンセルされます。.. したがって、明確な積分ではCを無視できます。
結果:






チェック:このような単純な形状で、ジオメトリによって面積を計算してみましょう:
a= 2+42 × 1 = 3
はい、それは3の面積を持っています。
(イェーイ!
: 次のように、角括弧内に不定積分(+Cなし)を表示できます。
例(続き)
あなたの答えを表示する良い方法:
別の例を試してみましょう:
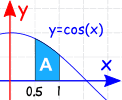
Example:
The Definite Integral, from 0.5 to 1.0, of cos(x) dx:
(Note: x must be in radians)
The Indefinite Integral is: ∫cos(x) dx = sin(x) + C
We can ignore C for definite integrals (as we saw above) and we get:
=
And another example to make an important point:
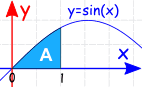
Example:
The Definite Integral, from 0 to 1, of sin(x) dx: 0
不定積分は次のとおりです。sin sin(x)dx=−cos(x)+C
0から行くので、Indefinite sin(x)dx=-cos(x)+C
0から行くので、Indefinite sin(x)dx=-cos(x)+C
x=1で積分を計算できますか?-cos(1)=-0.540…何?
何?
何? それは否定的ですか? しかし、それはグラフで肯定的に見えます。
まあ。.. 私たちは間違いを犯しました! x=0で積分を減算する必要があるためです。
私たちはそれがゼロであると仮定すべきではありません。
だから、私たちは他から一方を減算し、適切にそれをやってみましょう: /div>
=
それは良いです!しかし、曲線が軸の下にあるとき、負の領域を持つことができます。
例:
cos(x)dxの1から3までの定積分:
そのうちのいくつかは正であることに注意してください。いくつかの否定的な。
定積分は正味値を計算します。
計算をしましょう。
計算をしましょう。:
=
ジャンプ-0.700の最終結果と正よりも負があります。…だから我々は覚えておくべきこの重要なことを持っています:
cos(x)を異なる開始値と終了値で積分してみて、正と負の動作を確認してくださ
正の領域
しかし、すべての領域を正として処理したい場合があります(軸の下の部分を減算せずに)。その場合、この例のように、領域を別々に計算する必要があります。

例: X=1からx=3までのy=cos(x)とx軸の間の総面積はいくらですか?これは今行った例のようなものですが、今はすべての領域が正であることを期待しています(ペイントしなければならなかったと想像してください)。
だから、我々は別々に部品を行う必要があります:
- X軸の上の領域のための一つ
- X軸の下の領域のための一つ
曲線は、x=π/2でx軸を横切るので、我々は持っている:
1からπ/2へ:
=sin(π/2)-sin(1)
π/2から3へ:
=sin(3)−sin(π/2)
最後のものは負になりますが、正にしたいので、
総面積=0.159。.. + 0.859… = 1.018…
これは前の例の答えとは非常に異なります。はい、積分している関数は、aとbの間で連続していなければなりません:穴、ジャンプ、または垂直漸近線(関数が無限大に向かって上下する)はありません。
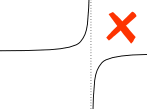
例:
aとbの間の垂直漸近線は定積分に影響します。P>
プロパティ
上の領域−下の領域
積分は軸の上の領域を加算しますが、”正味値”の場合は下の領域を減算します: p>
関数の追加
f+gの積分は、fの積分にgの積分に等しいf+gの積分に等しいf+gの積分に等しいf+gの積分に等しいf+gの積分に等しいf+gの積分に等しいf+gの積分に等しいf+gの積分に等しいf+gの積分に等しいf+gの積分に等しいf+gの積分に等しいf+gの積分に等しいf+gの積分に等しいf+gの積分に等しいf+gの積分に等しいf+gの積分に等しいf+gの積分に等しい:
間隔の方向を反転すると、元の方向の負の値が得られます。p>
![]()

Leave a Reply