古い問題は新しい洞察をもたらしますか? おそらく4色定理の優雅な証明?4色問題は、最も有名な数学的問題の1つです。
最終的には、有効な証明がありましたが、コンピュータ時間の千時間以上に依存していたもの。 Jim Tilleyの研究は、劇的な単純化が最終的に可能である可能性があることを示唆しています。 彼は、4色定理の最小反例が示さなければならないという性質、ケンペ-ロックを発見し、広範な調査に基づいて、バーコフ-ダイヤモンドが唯一の基本的なケンペ-ロック構成であるという推測を定式化した。
グラフの色付けは、グラフとして知られている数学的オブジェクトの頂点にラベル、または色を割り当てることを含みます。 4色問題は、代数グラフ理論の発展のための元の動機の一つを提供しました。 グラフカラーリングは、スポーツイベントのスケジュール設定、検査の時刻表の計画、座席計画の整理など、多くの現実世界の問題で使用されています。 また、数独パズルの基礎を提供します。
4色問題
有名な英国の数学者で論理学者のオーガスタス-ド-モルガンの学生であるフランシス-ガスリーは、1852年に4色問題を提起した。 彼は、穴を含まず、すべての領域(国や州など)を接続して、2つ以上の連続していない部分に領域が存在しないようにするなど、特定の条件を満たす地図 ガスリーは、このような地図では、隣接する二つの地域が同じ色ではないように地図を着色するために四つ以上の色を取ることは決してないと主張した。
今日では、4色の問題はグラフの観点から表現され、マップの領域を着色する代わりに、グラフの頂点を着色します。 4色定理のすべての既存の証明は、最小の反例が存在できないことを示しています。 (最小反例は、頂点を適切に着色するために4色以上を必要とする最小の平面グラフです。 三角形分割ではないグラフは、辺を挿入することによって1つに変換できるため、三角形分割である平面グラフのみを考慮する必要があります。 結果の三角形分割が4色対応の場合、元のグラフも4色対応になります。 自分の精査を三角測量に制限することができることは非常に便利です。

証明を提供した人たちの証明
の初期の試みは、英語の弁護士でアマチュア数学者であるアルフレッド-ブレイ-ケンペは、彼の失敗した努力によって評判が最も汚染された人物であった。 彼は1879年に彼の成功を発表し、彼の’証明’数学のアメリカのジャーナルに掲載されました。 11年後、しかし、別の英語の数学者、パーシー Heawoodは、彼がその最終的な領域のためにケンペの方法が失敗したような方法で、最終的な領域まで4色の地図を作成しました。 彼の失敗にもかかわらず、Kempeは便利なツール–Kempeチェーンを残しました。 これは、すべての頂点が正確に2つの色を使用する最大の接続された(辺に沿ったパスによって他の頂点から到達可能なすべての頂点)部分グラフです。 Kempeの鎖は着色および再着色のグラフで器械を証明した。 図1を参照してください。
バーコフのダイヤモンドだけが4色の可能性の鍵であれば、それは驚異的な単純化になります。
最初の有効な証明は1976年にKenneth AppelとWolfgang Hakenによって発表されました。 それは彼らの引数の特定の側面を検証するために、コンピュータの時間の千時間以上を必要としました。 潜在的に人為的なエラーを含むコンピュータコードに依存するというこの概念(そして彼らのコードはやった!)は、「人間の」証明ではなく、数学的コミュニティの大部分を満足していません。 AppelとHakenの証明は全体的な構造でエレガントでしたが、詳細は醜いものでした。 証明は1996年にRobertson、Sanders、Seymour、Thomasの4人の数学者のチームによって洗練されましたが、彼らはまだ証明を完了するためにコンピュータコードに依存していました。 2010年、スタインバーガーは別のバリエーションを提供した。 しかし、なぜ4色定理が真であるのかについては、まだ完全に満足のいく答えはありません。 (予想が証明されると、それはa’定理の地位を得ました。’)

とアマチュア数学者。
代替証明の検索
4色の問題は、それがアマチュア数学者の何千もの関心を集めていることを明確にし、理解するのはとても簡 1978年から1984年までカナダの王立軍事大学の物理学者で校長を務めていたジム-ティリーの父親は、そのような夢想家の一人でした。 彼は突破口を作ったと感じたときはいつでも、彼は彼の息子、ジムに彼の仕事をチェックするように頼むだろう。 ジムはいつも欠陥を見つけた しかし、彼の父の努力が実を結ぶだろうという彼の最初の懐疑主義にもかかわらず、彼は4色の問題に対する熱意に感染し、それを激しく研究し始め
ケンペ-ロック
ジム-ティリーの研究は、4色定理への最小反例が示さなければならないという新しい性質を発見することにつながった。 彼はそれを”Kempe-locking”と命名しました。”彼は、最小の反例が示さなければならない別の特性と互換性がない可能性が高いことに気づいた–すなわち。、グラフがどのように接続されているか(それが崩壊する前にグラフから削除する必要がありますどのように多くの頂点)。
TilleyのKempe-lockingは、三角形分割の辺に関連付けられたプロパティです。 この概念は、隣接する頂点xとyの間のエッジxyを削除することから始まります。 結果として得られるグラフのすべての4色に対して、xとyの色が同じである場合、Xの色がyの色と異なる原因となるケンペ鎖上の色交換の列が存在しない場合、元の三角形分割はエッジxyに関してケンペロックされていると言われる。 ティリーは、4色定理に対する最小反例は、その辺のすべてに関してケンペロックされなければならないことを証明した。
Kempe-lockingは特に制限的な条件であり、三角測量が大きくなるにつれて満たすことがより困難になります。 ティリーは、ケンペロックされたエッジを持つ三角形分割に共通するものがあるかどうかを発見するために着手しました。 彼の最も初期のケンペロックの探索は、彼をBirkhoff diamondに導いた。

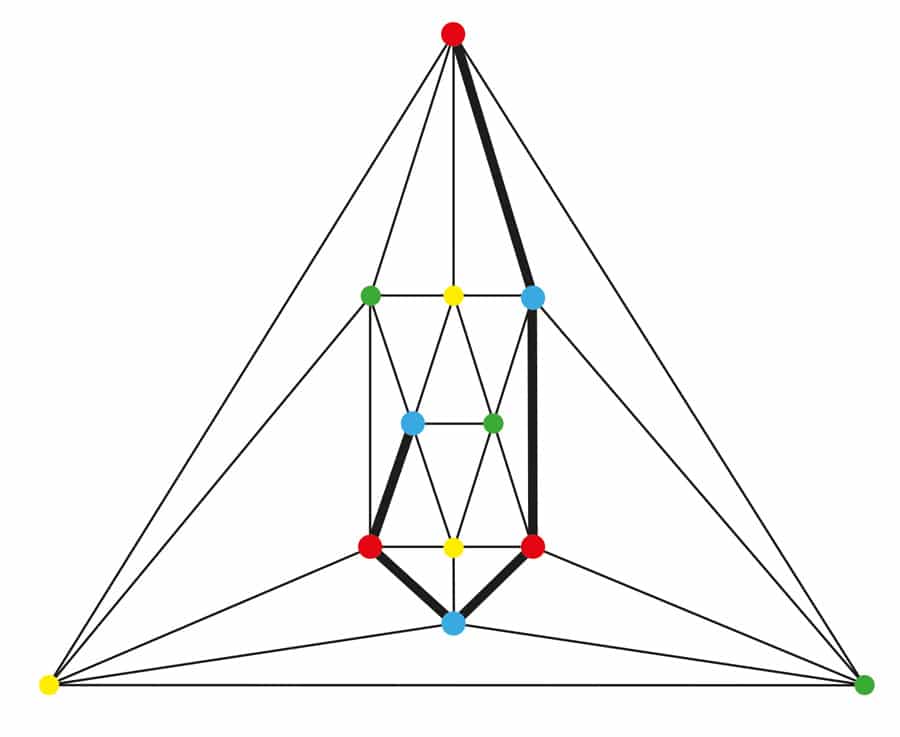
図3. 二つの平面グラフ、一つは6つの頂点上の4接続された三角形分割と一つは17の頂点上の5接続された三角形分割。
バーコフダイヤモンド
1913年、G.D.バーコフは、マップ内の十カ国の特定の構成(四つの国のセットを囲む六つの国の境界リング)が重要な特性を持っていることを発見した。 その構成がマップ内に存在し、その構成が削除されたサブマップが4色対応である場合、マップ全体が4色対応になります。 したがって、最小反例はその特定の構成を含めることはできません。 それはBirkhoffのダイヤモンドとして知られることを来た。 Tilleyは、Xとyがバーホフダイヤモンドのグラフ版の端点でもある場合にのみ、Kempeロックされたエッジxyが発生するように見えることを発見しました。 図2を参照してください。
この予想は簡単に述べられ、理解でき、興味深いものであり、すべての平面グラフが4-colorableである理由について説得力のある説明を提供しています。
バーホフダイヤモンドのないケンペロッキング構成に遭遇したことがない彼は、バーホフダイヤモンドが唯一の”基本的な”ケンペロッキング構成であり、サブグラフとしてより小さなケンペロッキング構成を含まないと推測した。 しかし、ティリーは彼の批判的な推測を証明できないことを発見した。 もし真であれば、予想は4色の定理を直接証明するので、それはイライラしていました。 (最小の反例にするには、三角測量にBirkhoff diamondサブグラフが含まれている必要がありますが、含まれている場合は最小の反例にはなりませんでした。)
圧倒的な支持ケース
彼の推測を証明する代わりに、Tilleyは次善のことをしました。 彼は実験主義者の役割を果たし、彼の推測を支持する圧倒的なケースを構築することに決めました。 彼はすべての関連する平面三角形分割を2つのクラスに分けた:グラフが崩壊する前に少なくとも4つの頂点を削除する必要があるもの(4-連結)と、グラフが崩壊する前に少なくとも5つの頂点を削除する必要があるもの(5-連結)。 図3を参照してください。 ティリーの広範な検索に役立つのは、彼が各同型クラス(構造的に同一のグラフ)の1つのメンバーだけを調べなければならなかったことでした。 ティリーは、最大15個の頂点上の4連結平面三角形分割の8,044個の同型クラスすべてと、最大24個の頂点上の5連結平面三角形分割の9,733個の同型クラスすべてを調べた。 彼は三つのケンペロックされた三角測量だけを発見した。 発見されたそれぞれのケンペロックされたエッジはバーコフのダイヤモンドを特徴とし、それぞれが4つの連結された三角測量で発生した。 5つの連結された三角形分割の中には全くなかった。

ティリーは、16頂点上のすべての30,926個の同型クラスと17頂点上のすべての158,428個の同型クラスを調べることによって、4連結三角形分割 計算時間の制限は、100,000個のランダムに生成された非同型三角形分割のサンプルに彼の検索を制限することを意味し、18,19、および20個の頂点上のクラ 展開された検索では、45個の追加のケンペロック三角形分割が行われましたが、元の検索とまったく同じ結果が得られました。ここからどこですか?
ここからどこですか?
ティリーの広範な検索は、バーコフのダイヤモンドが基本的なケンペロック構成であることを容易に確認しました。 彼は彼の推測を徹底的にテストしましたが、それは証明されていません。 ティリーの予想が真実であることが証明された場合、すなわち、バーコフのダイヤモンドだけが4色性の鍵であることが証明された場合、それは問題の驚異的な単純化になるでしょう:それをすべて説明する単一の構成-数学的優雅さ。p>

4色の推測を証明するには、多くの著名な数学者の努力が必要でした。 バーコフのダイヤモンドが唯一の基本的なケンペロック配置であるというティリーの予想は、証明するのがさらに難しいかもしれません。 しかし、実験的証拠は強い。 理論家は言うかもしれない”なぜ気にするか。”結局のところ、予想は簡単に述べられ、理解でき、興味深いものであり、すべての平面グラフが4色である理由について説得力のある説明を提供します。”
個人的な反応
最初に4色の問題に対する熱意を促し、それを激しく勉強するように導いたのは何ですか?
それは彼の退職の問題と彼のアイデアのためのサウンドボードとして私を使用する彼の欲求と私の父の強迫観念でした。この分野での今後の研究の計画は何ですか?
私は最近、4色の問題に対する全く異なるアプローチを含む複雑な論文を見直しました。 紙が立っているように、私はそれが欠陥を持っていると信じています。 しかし、それは約束を持っています。 私は共同を探検するように誘惑されるかもしれない。
div
Leave a Reply