フィボナッチ数列は数の系列です。

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …

次の数は、その前に二つの数字を合計することによって発見されます：

• 2は、それの前に二つの数字を追加することによって発見されます（1+1）、
• 3は、それの前に二つの数字を追加することによって発見されます（1+2）、
• 5は（2+3）、
• というように！例：上記のシーケンスの次の数は21+34=55です。

  それは簡単です！ここに長いリストがあります

  :

  0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, …あなたは次のいくつかの数字を把握できますか？

  これらの幅の正方形を作ると、素敵なスパイラルが得られます。

  

  正方形がどのようにきれいに
  たとえば、5と8は13を、8と13は21を、というようにします。

  
  このスパイラルは自然の中で発見されました！
  参照: 自然、黄金比、フィボナッチ

  ルール

  フィボナッチ数列は”ルール”として書くことができます（シーケンスとシリーズを参照）。

  最初に、用語は次のように0から番号が付けられます:

  n =	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	。..
  xn =	0	1	1	2	3	5	8	13	21	34	55	89	144	233	377	。..

  したがって、用語番号6はx6（8に等しい）と呼ばれます。

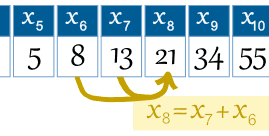
  例：8番目の項は 7番目の項に6番目の項を加えたものです。 x8=x7+x6

  だから、我々はルールを書くことができます：

  ルールはxn=xn−1+xn−2

  ここで、:

  • xnは項番号”n”です
  • xn−1は前の項（n−1）です
  • xn−2はその前の項（n−2）です

  例：項9は次のように計算されます。

  x9=x9−1+x9−2

  =x8+x7

  =21+13

  =34

  黄金比

  

  そして、ここで驚きです。 任意の2つの連続した（次々に）フィボナッチ数を取るとき、それらの比は約1.618034である黄金比”φ”に非常に近い。..

  In fact, the bigger the pair of Fibonacci Numbers, the closer the approximation. Let us try a few:

  ..

  A	B		B / A
  2	3		1.5
  3	5		1.666666666…
  5	8		1.6
  8	13		1.625
  …	…		…
  144	233		1.618055556…
  233	377		1.618025751…
  …	…

  私たちは2と3で始める必要はありません、ここで私はランダムに192と16を選192, 16, 208, 224, 432, 656, 1088, 1744, 2832, 4576, 7408, 11984, 19392, 31376, …):

  ..良い値を得るには時間がかかりますが、フィボナッチ数列だけではこれを行うことができないことを示しています！

  黄金比を使用してフィボナッチ数を計算する

  さらに驚くべきことは、黄金比を使用して任意のフィボナッチ数を計算できることです。

  xn=φ n−(1−φ)n≤5

  答えは整数として出てきます。前の二つの項の加算とまったく同じです。

  例:x6

  x6=(1.618034…)6 − (1−1.618034…私はこれに電卓を使用したとき（小数点以下6桁に黄金比を入力するだけ）、私は答え8.00000033を得た、より正確な計算は8に近いでしょう。試してみてくださいn=12そして、あなたが得るものを見てください。

  また、前のフィボナッチ数に黄金比を掛け、四捨五入することでフィボナッチ数を計算することもできます（1より上の数で動作します）。

  例：8×φ=8×1.618034。.. = 12.94427… =13(四捨五入)

  いくつかの興味深いもの

  ここで再びフィボナッチ数列です:

  A	B		B / A
  192	16		0.08333333…
  16	208		13
  208	224		1.07692308…
  224	432		1.92857143…
  …	…		…
  7408	11984		1.61771058…
  11984	19392		1.61815754…
  …	…

  n =	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	。..
  xn =	0	1	1	2	3	5	8	13	21	34	55	89	144	233	377	610	。..