ヒストグラム
棒グラフ、頻度分布、およびヒストグラム
頻度分布、棒グラフ、およびcircleグラフ
特定のイベントの頻度は、イベントが発生 相対頻度は、カテゴリ内の観測された応答の割合。
例：私たちは、自分の車がどの国であるかを学生に尋ねました（または車がない）から、答えの集計を行います。 次に、各カテゴリの頻度と相対的な頻度を計算しました。 Relativefrequencyは、周波数をresponentsの総数で除算することによって計算されます。 The following tablesummarizes.
| Country | Frequency | Relative Frequency |
| US | 6 | 0.3 |
| Japan | 7 | 0.35 |
| Europe | 2 | 0.1 |
| Korea | 1 | 0.05 |
| None | 4 | 0.2 |
| Total | 20 | 1 |
Below is a bar graph for the car data. This bar graph is called a Paretochart since the height represents the frequency. バーの幅は常に同じであることに注意してください。p>
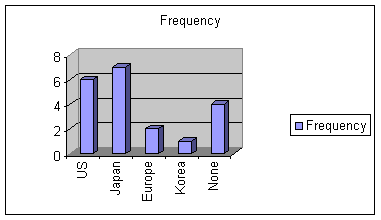
私たちは、周波数に比例したサイズの円にウェッジを配置することによって、このデータの円グラフと呼ばれる円グラフを作
以下はこのデータを示している円グラフです。
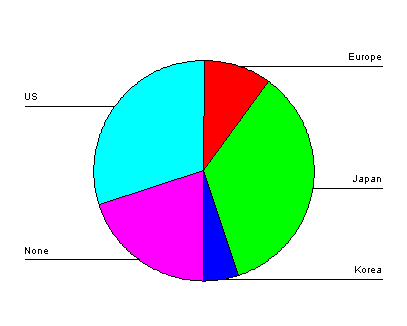
各スライスの角度を見つけるには、式を使用します
たとえば、私たちの車の角度を見つけるには、
6
Angle=x360=108度
20
ヒストグラム
ヒストグラムは、垂直座標が周波数カウントであり、水平座標が対応する棒グラフです数値間隔に。
例：
タホ湖の透明度の深さは、いくつかの異なる場所で測定されました次のようにインチでの結果：
15.4, 16.7, 16.9, 17.0, 20.2, 25.3, 28.8, 29.1, 30.4, 34.5,
36.7, 39.1, 39.4, 39.6, 39.8, 40.1, 42.3, 43.5, 45.6, 45.9,
48.3, 48.5, 48.7, 49.0, 49.1, 49.3, 49.5, 50.1, 50.2, 52.3
We use a frequency distribution table with class intervals of length 5.
| Class Interval | Frequency | Relative Frequency | Cumulative Relative Frequency |
| <20 | 4 | 0.129 | 0.129 |
| <25 | 1 | 0.032 | 0.161 |
| < 30 | 3 | 0.097 | 0.258 |
| < 35 | 2 | 0.065 | 0.323 |
| < 40 | 6 | 0.194 | 0.516 |
| < 45 | 3 | 0.097 | 0.613 |
| < 50 | 9 | 0.290 | 0.903 |
| < 55 | 3 | 0.097 | 1.000 |
| Total | 31 | 1.000 |
以下はヒストグラムのグラフです
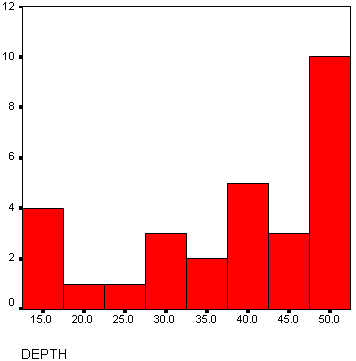
ヒストグラムの形状
ヒストグラム二つのこぶがある場合は二峰性、多くのこぶがある場合は多峰性。 非対称ヒストグラムは、対称でない場合は歪んだヒストグラムと呼ばれます。 上の尾が下の尾よりも長い場合、それは陽性である。 上の尾がそれよりも短い場合は否定的に斜めになっています。
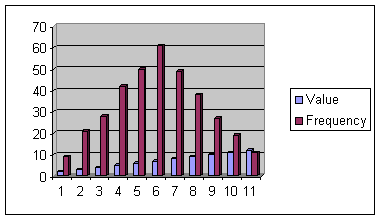Unimodal,Symmetric, Nonskewed
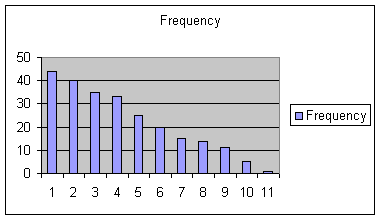Nonsymmetric,Skewed Right
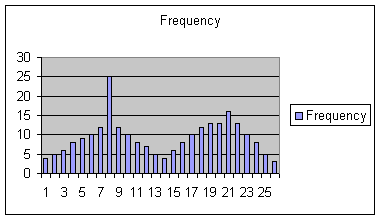Bimodal
Leave a Reply