映画”星間”の興行成功により、多くの人々は星間輸送の手段としてのワームホールの見通しに興奮しています。 現在のところ、このようなエキゾチックな物体が自然界に存在するという証拠はないが、おそらく高次元の弦理論と基本的な時空泡の工学のバージョンから、人工的に作成される可能性がある。 ワームホール研究は、今日、毎年査読されたジャーナルに数十の論文が掲載されているエキサイティングなテーマですが、その起源を思い出すことは価値があ

1915年にアルバート-アインシュタインは、オブジェクトがお互いを引き付け、それらの周りの空間と時間にどのように影響するかをきれいに定義する重力の彼の説明、相対性理論の彼の一般的な理論を発表しました。 何年もの間、アメリカの物理学者ジョン・ウィーラーは、「宇宙はどのように動くかを物質に伝え、物質はどのように曲線を描くかを空間に伝えます」というフレーズをコインにしました。 アインシュタインは、時空の曲率の現れとして重力を説明しました。 一般相対性理論は、量子力学につながった物質の粒子理論とは対照的に、連続場の理論です。

アインシュタインはまた、量子力学、サブ原子粒子を記述する理論の開発に関与していました。 しかし、彼はその固有の不確実性と確率的性格に完全に満足していませんでした。 そこで1935年にネイサン・ローゼンと共同で一般相対性理論を用いて電子の場の理論を作った。 彼らの論文は”一般相対性理論における粒子問題”と題されていた。 アインシュタインとローゼンは、場の不連続性（特異点）を除いて、一般相対性理論とマクスウェルの電磁理論の記述（メトリック）以外の他の変数を使用しない物質と電気の原子論の可能性を調査していた。 結果の1つは、最も基本的な荷電粒子がゼロ質量の1つであることが判明したことでした。

最後に、彼らが制作したものは非常にオリジナルのものでした。 Black ds^2=-\dfrac{1}{1-2m/r}dr^2-r^2（d\theta^2+\sin^2\theta d\phi^2）+（1-2m/r）dt^2dt

ここで、\（ds^2\）はメトリックであり、\（m=gm/C^2\）はメトリックです。dt ds^2=-\dfrac{1}{1-2m/r}dr^2-r^2（d\theta^2+\sin^2\theta d\phi^2）+（1-2m/r）dt^2dt

ここで、\（ds^2\）はメトリックであり、\（m=gm/C^2\）はメトリックである。球面座標\((r,\theta,\phi)\)と時間\(t\)を使用しています。

彼らは、曲率特異性、ブラックホールによって暗示される空間曲率の不連続性および同様の現象を含む領域を除去するために座標変換を行った。 Coordinate dS^2=-4（u^2+2m）du^2-（u^2+2m）d2d\omega^2+\dfrac{u^2}{u^2+2m}dt^2dt

ここで、d d\omega^2=d\theta^2+\sin^2\theta^2+\sin^2\theta^2+\sin^2\theta^2dtは、coordinate u^2=r-2m duとremoved u^2=r-2m duを意味します。シータd\ファイ^2\）。

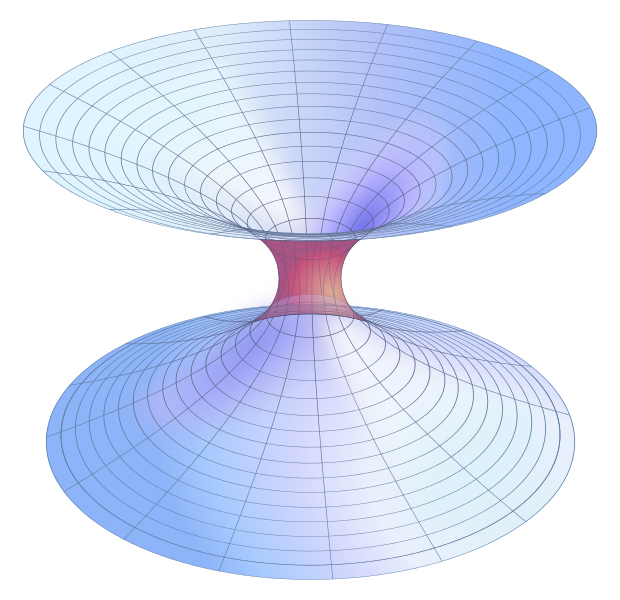
この解は、橋または”喉”を持つシュヴァルツシルトワームホールで接続された二つの漸近的に平坦なシートの空間による物理空間の数学的表現でした。 これは、二つのシートと、類推によって、実際の、三次元、宇宙の二つの別々の部分を接続します。 図1は、ワームホールの周りの空間を示しており、無限大にズームアウトすると上下の空間が”エッジ”で平らになります。

これは横断可能なワームホールではなかったので、1950年代の物理学者John Wheelerと1980年代のKip Thorneの到着を待たなければならなかった。 1987年、カール・セーガンの小説「Contact」（後の長編映画）の奨励により、ソーンと同僚のマイケル・モリスは、球対称で静的なワームホールを実数で有限の円周で記述するための数学的記述、計量を構築することができた。 これは、最小湾曲空間での負の無限大から、喉が位置する最小値に減少し、その後、異なる最小湾曲空間で喉から正の無限大に増加する座標を有していた。 この解は、ブラックホールとは異なり、事象の地平線を持たないという特徴を持っています。 Thorne and Morrisの論文は「時空のワームホールと星間旅行のためのそれらの使用：一般相対性理論を教えるための道具」と題されていた。 この論文は、学術調査の新しい領域としてワームホール研究を確立するのに役立った。

それ以来、多くの論文が出版されており、実際には天文調査が行われており、自然のワームホールを探して最も遠い星や銀河を調べています。 アインシュタイン-ローゼン橋は横断可能なワームホールではなく、著者の意図ではありませんでしたが、ワームホールの最初の数学的記述を生み出しました。 彼らはこれのために記憶されるべきです。 科学研究は、多くの場合、はるかに研究者の本来の意図を超えて到達する含意と非常に予想外の何かを生成します。

ケルビンF. Long

この記事が出版されて以来、私たちの雑誌Principiumは、ワームホールとアインシュタイン-ローゼン橋についてより詳細に議論する二つの問題（issues9&10）を これらの問題はまた、英国惑星間協会と共同で星間研究のためのイニシアチブが主催する”星間ワームホール：物理学と実践的な実現”に関する一日のシン

div