Un vieux problème donnera-t-il un nouvel aperçu? Peut-être une preuve élégante du théorème des 4 couleurs?
Le problème des 4 couleurs est l’un des problèmes mathématiques les plus célèbres. Il a résisté à la preuve pendant plus de cent ans avant de finalement succomber; à la fin, il y avait une preuve valable, mais qui reposait sur plus de mille heures de temps informatique. Les recherches de Jim Tilley suggèrent qu’une simplification spectaculaire pourrait finalement être possible. Il a découvert une propriété, le verrouillage de Kempe, qu’un contre-exemple minimum au théorème des 4 couleurs doit présenter et a formulé une conjecture, basée sur des recherches approfondies, selon laquelle le diamant de Birkhoff est la seule configuration fondamentale de verrouillage de Kempe.
La coloration de graphe consiste à attribuer des étiquettes, ou des couleurs, aux sommets d’un objet mathématique connu sous le nom de graphe. Le problème des 4 couleurs a fourni l’une des motivations originales pour le développement de la théorie algébrique des graphes. La coloration graphique est utilisée dans de nombreux problèmes réels, tels que la minimisation des conflits lors de la planification d’événements sportifs, la planification des horaires d’examen et l’organisation des plans de sièges, même pour le placement de caméras de vidéosurveillance dans un bâtiment avec de nombreux coins afin de minimiser le chevauchement des caméras. Il fournit également la base pour les puzzles de Sudoku.
Le problème des 4 couleurs
Francis Guthrie, un étudiant du célèbre mathématicien et logicien britannique Augustus De Morgan, a posé le problème des 4 couleurs en 1852. Il a formulé le problème en ce qui concerne les cartes qui satisfont à certaines conditions, telles que ne pas contenir de trous et avoir chaque région (par exemple un pays ou un État) connectée de sorte qu’aucune région n’existe en deux parties non contiguës ou plus. Guthrie a affirmé que pour de telles cartes, il ne faudrait jamais plus de quatre couleurs pour colorer la carte de sorte qu’il n’y ait pas deux régions voisines de la même couleur.
De nos jours, le problème des 4 couleurs s’exprime en termes de graphiques, et au lieu de colorer les régions dans les cartes, on colore les sommets dans les graphiques. Toutes les preuves existantes du théorème des 4 couleurs démontrent qu’un contre-exemple minimum ne peut pas exister. (Un contre-exemple minimum est le plus petit graphe plan qui nécessite plus de quatre couleurs pour une coloration correcte de ses sommets.) Seuls les graphes planaires qui sont des triangulations doivent être pris en compte, car tout graphe qui n’est pas une triangulation peut être transformé en un seul en insérant des arêtes. Si la triangulation résultante est à 4 couleurs, alors le graphe d’origine est également à 4 couleurs. Il est très utile de pouvoir limiter son examen aux triangulations.

Une première tentative de preuve
Parmi ceux qui ont offert une preuve, Alfred Bray Kempe, un avocat anglais et mathématicien amateur, était la personne dont la réputation était la plus entachée par son effort raté. Il a annoncé son succès en 1879 et sa « preuve » a été publiée dans l’American Journal of Mathematics. Onze ans plus tard, cependant, un autre mathématicien anglais, Percy Heawood, a créé une carte qu’il a colorée jusqu’à la région finale de telle sorte que la méthode de Kempe a échoué pour cette région finale. Malgré son échec, Kempe a laissé un outil utile – une chaîne Kempe. C’est un sous-graphe maximal, connecté (chaque sommet accessible de tout autre par un chemin le long des arêtes) dans lequel tous les sommets utilisent exactement deux couleurs. Les chaînes de Kempe ont joué un rôle déterminant dans la coloration et la re-coloration des graphiques. Voir Figure 1.
Ce serait une simplification étonnante
si le diamant Birkhoff seul est la clé de la 4-colorabilité.
Preuve enfin
La première preuve valide a été annoncée en 1976 par Kenneth Appel et Wolfgang Haken. Il a fallu plus de mille heures de temps informatique pour vérifier des aspects particuliers de leur argument. Cette notion de s’appuyer sur du code informatique, contenant potentiellement des erreurs d’origine humaine (et leur code l’a fait!), plutôt qu’une preuve « humaine », n’a pas satisfait une grande partie de la communauté mathématique. La preuve d’Appel et Haken était élégante dans sa structure globale, mais les détails étaient laids.
La preuve a été affinée en 1996 par une équipe de quatre mathématiciens: Robertson, Sanders, Seymour et Thomas, mais ils se sont toujours appuyés sur le code informatique pour compléter leur preuve. En 2010, Steinberger a proposé une autre variante. Cependant, il n’y a toujours pas de réponse complètement satisfaisante quant à la raison pour laquelle le théorème des 4 couleurs est vrai. (Une fois la conjecture prouvée, elle a acquis le statut de théorème.’)

et mathématicien amateur.
La recherche d’une preuve alternative
Le problème des 4 couleurs est si facile à articuler et à comprendre qu’il a suscité l’intérêt de plusieurs milliers de mathématiciens amateurs, croyant tous pouvoir trouver une preuve classique simple et ainsi devenir célèbre. Le père de Jim Tilley, physicien et directeur du Collège militaire royal du Canada de 1978 à 1984, était l’un de ces rêveurs. Chaque fois qu’il sentait qu’il avait fait une percée, il demandait à son fils, Jim, de vérifier son travail. Jim a toujours trouvé une faille. Pourtant, malgré son scepticisme initial quant au fait que les efforts de son père porteraient jamais leurs fruits, il a été infecté par un enthousiasme pour le problème des 4 couleurs et a commencé à l’étudier intensément.
Kempe-locking
Les recherches de Jim Tilley ont conduit à sa découverte d’une nouvelle propriété qu’un contre-exemple minimum au théorème des 4 couleurs doit présenter. Il l’a nommé Kempe-locking. »Il s’est rendu compte qu’il était susceptible d’être incompatible avec une autre propriété qu’un contre–exemple minimum doit présenter – à savoir., comment un graphe est connecté (combien de sommets doivent être supprimés d’un graphe avant qu’il ne s’effondre).
Le Kempe-locking de Tilley est une propriété associée à une arête dans une triangulation. La notion commence par la suppression d’une arête xy entre les sommets adjacents x et y. Si pour chaque 4-coloration du graphe résultant dans laquelle les couleurs de x et y sont identiques, il n’y a pas de séquence d’échanges de couleurs sur les chaînes de Kempe qui fait que la couleur de x diffère de la couleur de y, alors la triangulation d’origine est dite verrouillée par Kempe par rapport à l’arête xy. Tilley a prouvé qu’un contre-exemple minimal au théorème des 4 couleurs doit être verrouillé par Kempe par rapport à chacune de ses arêtes ; chaque arête d’un contre-exemple minimal doit avoir cette propriété de coloration.
Le verrouillage de Kempe est une condition particulièrement restrictive qui devient plus difficile à satisfaire à mesure qu’une triangulation s’agrandit. Tilley a entrepris de découvrir s’il y a quelque chose de commun aux triangulations qui ont des bords verrouillés par Kempe. Sa première recherche de Kempe-locking l’a conduit au diamant Birkhoff.

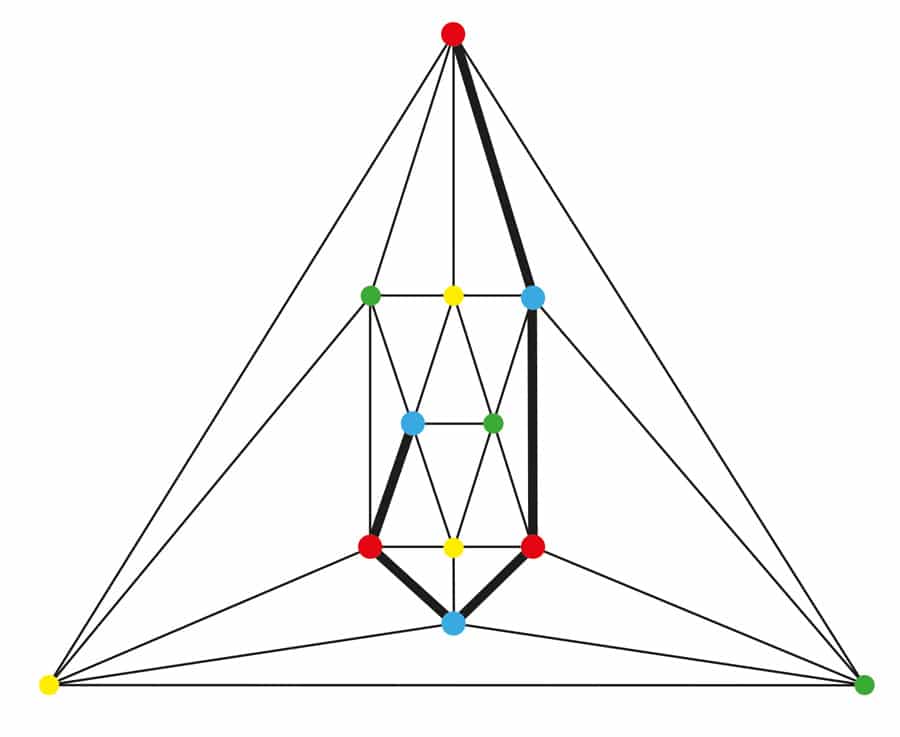
Figure 3. Deux graphes planaires, une triangulation à 4 connexions sur 6 sommets et une triangulation à 5 connexions sur 17 sommets.
Le diamant de Birkhoff
En 1913, G. D. Birkhoff a découvert qu’une certaine configuration de dix pays sur une carte (un anneau limite de six pays qui entoure un ensemble de quatre pays) a une propriété importante. Si cette configuration est présente dans une carte et si la sous-carte avec cette configuration supprimée est à 4 couleurs, alors la carte entière sera à 4 couleurs. Ainsi, un contre-exemple minimum ne peut pas contenir cette configuration particulière. Il est devenu connu sous le nom de diamant Birkhoff. Tilley a découvert qu’une arête xy verrouillée par Kempe ne semble apparaître que lorsque x et y sont également les points finaux de la version graphique d’un diamant de Birkhoff. Voir Figure 2.
La conjecture est facile à énoncer, compréhensible et intrigante, et offre une explication convaincante de la raison pour laquelle tous les graphes planaires sont à 4 couleurs.
N’ayant rencontré aucune configuration de verrouillage de Kempe sans diamant de Birkhoff, il a conjecturé que le diamant de Birkhoff est la seule configuration de verrouillage de Kempe « fondamentale », qui ne contient pas une configuration de verrouillage de Kempe plus petite en tant que sous-graphe. Cependant, Tilley a constaté qu’il ne pouvait pas prouver sa conjecture critique. C’était frustrant car, si elle était vraie, la conjecture prouverait directement le théorème des 4 couleurs. (Pour être un contre-exemple minimum, une triangulation devrait contenir un sous-graphe de diamant de Birkhoff, mais si c’était le cas, ce ne pourrait pas être un contre-exemple minimum.)
Un cas à l’appui accablant
Au lieu de prouver sa conjecture, Tilley a fait la meilleure chose qui soit. Il a décidé de jouer le rôle d’un expérimentateur et de construire un cas accablant pour étayer sa conjecture. Il a divisé toutes les triangulations planaires pertinentes en deux classes: celles dans lesquelles au moins quatre sommets doivent être supprimés avant que les graphes ne s’effondrent (4-connectés) et celles dans lesquelles au moins cinq sommets doivent être supprimés avant que les graphes ne s’effondrent (5-connectés). Voir Figure 3. Utile dans la recherche approfondie de Tilley était qu’il ne devait examiner qu’un seul membre de chaque classe d’isomorphisme (graphes structurellement identiques). Tilley a examiné les 8 044 classes d’isomorphisme de triangulations planaires à 4 connexions sur un maximum de 15 sommets et les 9 733 classes d’isomorphisme de triangulations planaires à 5 connexions sur un maximum de 24 sommets. Il n’a trouvé que trois triangulations verrouillées par Kempe. Chaque bord découvert verrouillé par Kempe comportait un diamant de Birkhoff et chacun s’est produit dans une triangulation à 4 connexions. Il n’y en avait pas du tout parmi les triangulations à 5 connexions.

Tilley a étendu sa recherche parmi les triangulations à 4 connexions en examinant les 30 926 classes d’isomorphisme sur 16 sommets et les 158 428 classes d’isomorphisme sur 17 sommets. Les limitations de temps de calcul signifiaient limiter sa recherche à des échantillons de 100 000 triangulations non isomorphes générées aléatoirement pour chacune des classes sur 18,19 et 20 sommets. La recherche élargie a permis d’obtenir 45 triangulations supplémentaires verrouillées par Kempe, mais exactement les mêmes résultats que la recherche originale: chaque bord verrouillé par Kempe dans une triangulation comportait un diamant Birkhoff associé.
Où d’ici ?
Les recherches approfondies de Tilley ont facilement confirmé que le diamant Birkhoff est une configuration fondamentale de verrouillage Kempe. Il a soigneusement testé sa conjecture, mais elle reste non prouvée. Si (ou quand) la conjecture de Tilley s’avère vraie, c’est-à–dire que le diamant de Birkhoff est à lui seul la clé de la 4-colorabilité, ce serait une simplification étonnante du problème: une configuration unique qui explique tout – l’élégance mathématique.

Prouver la conjecture à 4 couleurs a nécessité les efforts de nombreux mathématiciens éminents. La conjecture de Tilley selon laquelle le diamant Birkhoff est la seule configuration fondamentale de verrouillage de Kempe peut être encore plus difficile à prouver. Cependant, les preuves expérimentales sont solides. Les théoriciens pourraient dire ‘pourquoi s’embêter? »La réponse de Tilley est que la curiosité insatiable l’emportera: « Après tout, la conjecture est facilement énoncée, compréhensible et intrigante, et offre une explication convaincante de la raison pour laquelle tous les graphes planaires sont à 4 couleurs. »
Réponse personnelle
Qu’est-ce qui a d’abord suscité votre enthousiasme pour le problème des 4 couleurs et vous a amené à l’étudier si intensément?
C’était l’obsession de mon père pour le problème à sa retraite et son désir de m’utiliser comme caisse de résonance pour ses idées.
Quels sont vos projets de recherche dans ce domaine ?
J’ai récemment passé en revue un article compliqué impliquant une approche totalement différente du problème des 4 couleurs. En l’état actuel du document, je crois qu’il a des défauts. Pourtant, il est prometteur. Je pourrais être tenté d’explorer une collaboration.
Leave a Reply