Séquence de Fibonacci
La séquence de Fibonacci est la série de nombres :
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …
Le nombre suivant est trouvé en additionnant les deux nombres qui le précèdent :
- le 2 est trouvé en ajoutant les deux nombres qui le précèdent (1+1),
- le 3 est trouvé en ajoutant les deux nombres qui le précèdent (1+2),
- le 5 est (2+3),
- et ainsi de suite!
Exemple : le nombre suivant dans la séquence ci-dessus est 21 +34 = 55
C’est aussi simple que ça!
Voici une liste plus longue:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, …
Pouvez-vous trouver les prochains chiffres?
Fait une spirale
Lorsque nous faisons des carrés avec ces largeurs, nous obtenons une belle spirale:
Voyez-vous comment les carrés s’emboîtent parfaitement?
Par exemple 5 et 8 font 13, 8 et 13 font 21, et ainsi de suite.

Cette spirale se trouve dans la nature!
Voir: La Nature, Le Nombre d’Or et Fibonacci
La Règle
La Séquence de Fibonacci peut être écrite comme une « Règle » (voir Séquences et Séries).
Tout d’abord, les termes sont numérotés à partir de 0 comme ceci:
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | … |
| xn = | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | … |
Le terme numéro 6 est donc appelé x6 (ce qui équivaut à 8).
|
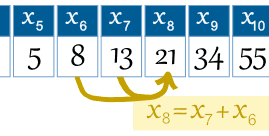
Exemple: le 8ème terme est x8= x7 + x6 |
 |
Afin que nous puissions écrire la règle:
La règle est xn =xn−1 + xn−2
où:
- xn est le nombre de termes « n »
- xn−1 est le terme précédent (n−1)
- xn−2 est le terme avant cela (n−2)
Exemple: le terme 9 est calculé comme ceci:
Nombre d’or
Et voici une surprise. Lorsque l’on prend deux nombres de Fibonacci successifs (l’un après l’autre) quelconques, leur rapport est très proche du Nombre d’Or « φ » qui est d’environ 1,618034…
In fact, the bigger the pair of Fibonacci Numbers, the closer the approximation. Let us try a few:
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
2
|
3
|
1.5 | |
|
3
|
5
|
1.666666666… | |
|
5
|
8
|
1.6 | |
|
8
|
13
|
1.625 | |
|
…
|
…
|
… | |
|
144
|
233
|
1.618055556… | |
|
233
|
377
|
1.618025751… | |
|
…
|
…
|
… |
Nous n’avons pas à commencer par 2 et 3, ici j’ai choisi au hasard 192 et 16 (et j’ai obtenu la séquence 192, 16, 208, 224, 432, 656, 1088, 1744, 2832, 4576, 7408, 11984, 19392, 31376, …):
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
192
|
16
|
0.08333333… | |
|
16
|
208
|
13 | |
|
208
|
224
|
1.07692308… | |
|
224
|
432
|
1.92857143… | |
|
…
|
…
|
… | |
|
7408
|
11984
|
1.61771058… | |
|
11984
|
19392
|
1.61815754… | |
|
…
|
…
|
… |
Il faut plus de temps pour obtenir de bonnes valeurs, mais cela montre que non seulement la séquence de Fibonacci peut le faire!
En utilisant Le Nombre d’Or pour Calculer les Nombres de Fibonacci
Et encore plus surprenant est que nous pouvons calculer n’importe quel Nombre de Fibonacci en utilisant le Nombre d’Or:
xn = φn−(1−φ) n√5
La réponse est un nombre entier, exactement égal à l’addition des deux termes précédents.
Exemple : x6
x6=(1.618034…)6 − (1−1.618034…) 6√5
Lorsque j’ai utilisé une calculatrice à ce sujet (en entrant uniquement le nombre d’or à 6 décimales), j’ai obtenu la réponse 8.00000033, un calcul plus précis serait plus proche de 8.
Essayez n = 12 et voyez ce que vous obtenez.
Vous pouvez également calculer un Nombre de Fibonacci en multipliant le nombre de Fibonacci précédent par le Nombre d’Or, puis en arrondissant (fonctionne pour les nombres supérieurs à 1):
Exemple: 8 × φ = 8 × 1.618034… = 12.94427… =13 (arrondi)
Quelques choses intéressantes
Voici à nouveau la séquence de Fibonacci:
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | … |
| xn = | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 | … |
Il existe un modèle intéressant:
- Regardez le nombre x3 = 2. Chaque 3ème nombre est un multiple de 2 (2, 8, 34, 144, 610, …)
- Regardez le nombre x4 =3. Chaque 4ème nombre est un multiple de 3 (3, 21, 144, …)
- Regardez le nombre x5 = 5. Chaque 5ème nombre est un multiple de 5 (5, 55, 610, …)
Et ainsi de suite (chaque nième nombre est un multiple de xn).
1/89 = 0,011235955056179775…
Notez que les premiers chiffres (0,1,1,2,3,5) sont la séquence de Fibonacci ?
D’une certaine manière, ils sont tous, sauf les nombres à plusieurs chiffres (13, 21, etc.) se chevauchent, comme ceci:
… etc …
0.011235955056179775… =1/89
Termes en dessous de Zéro
La séquence fonctionne également en dessous de zéro, comme ceci:
| n = | … | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| xn = | … | −8 | 5 | −3 | 2 | −1 | 1 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | … |
(Prouvez-vous que chaque nombre est trouvé en additionnant les deux nombres qui le précèdent!)
En fait la séquence en dessous de zéro a les mêmes nombres que la séquence au-dessus de zéro, sauf qu’ils suivent un +-+-… modèle. Cela peut être écrit comme ceci:
x−n =(-1) n + 1 xn
Qui dit que le terme « −n » est égal à (-1) n + 1 fois le terme « n », et la valeur (-1) n + 1 fait parfaitement le bon +1, -1, +1, -1, … modèle.
Histoire
Fibonacci n’était pas le premier à connaître la séquence, elle était connue en Inde des centaines d’années auparavant !

À propos de Fibonacci L’Homme
Son vrai nom était Leonardo Pisano Bogollo, et il a vécu entre 1170 et 1250 en Italie.
« Fibonacci » était son surnom, qui signifie à peu près « Fils de Bonacci ».
En plus d’être célèbre pour la séquence de Fibonacci, il a contribué à la diffusion des Chiffres hindous-arabes (comme nos nombres actuels 0, 1, 2, 3, 4, 5, 6, 7, 8, 9) à travers l’Europe à la place des Chiffres romains (I, II, III, IV, V, etc.). Cela nous a évité beaucoup de problèmes! Merci Leonardo.

Jour de Fibonacci
Le jour de Fibonacci est le 23 novembre, car il a les chiffres « 1, 1, 2, 3 » qui fait partie de la séquence. Alors le 23 novembre prochain, faites savoir à tout le monde!


Leave a Reply