Rational Exponents
Rational Exponents
Learning Objective(s)
· Convert radicals to expressions with rational exponents.
· Convert expressions with rational exponents to their radical equivalent.
· Use the laws of exponents to simplify expressions with rational exponents.
· Use rational exponents to simplify radical expressions.
Introduction
Les racines carrées sont le plus souvent écrites en utilisant un signe radical, comme ceci, ![]() . Mais il existe une autre façon de représenter la prise d’une racine. Vous pouvez utiliser des exposants rationnels au lieu d’un radical. Un exposant rationnel est un exposant qui est une fraction. Par exemple,
. Mais il existe une autre façon de représenter la prise d’une racine. Vous pouvez utiliser des exposants rationnels au lieu d’un radical. Un exposant rationnel est un exposant qui est une fraction. Par exemple, ![]() peut être écrit comme
peut être écrit comme ![]() .
.
Vous ne pouvez pas imaginer élever un nombre à un exposant rationnel? Ils peuvent être difficiles à s’y habituer, mais les exposants rationnels peuvent en fait aider à simplifier certains problèmes. Explorons la relation entre les exposants rationnels (fractionnaires) et les radicaux.
Réécrire des expressions radicales En utilisant des Exposants Rationnels
Les radicaux et les exposants fractionnaires sont des moyens alternatifs d’exprimer la même chose. Vous avez déjà vu comment les racines carrées peuvent être exprimées en exposant à la puissance de la moitié.
|
Radical Form |
Exponent Form |
Integer |
|
|
|
4 |
|
|
|
5 |
|
|
|
10 |
Let’s look at some more examples, but this time with cube roots. Rappelez-vous, le cubage d’un nombre l’élève à la puissance de trois. Notez que dans ces exemples, le dénominateur de l’exposant rationnel est le nombre 3.
|
Radical Form |
Exponent Form |
Integer |
|
|
|
2 |
|
|
|
5 |
|
|
|
10 |
These examples help us model a relationship between radicals and exposants rationnels : à savoir que la nième racine d’un nombre peut être écrite comme ![]() ou
ou ![]() .
.
|
Radical Form |
Exponent Form |
|
|
|
|
|
|
|
|
|
|
… |
… |
|
|
|
When faced with an expression contenant un exposant rationnel, vous pouvez le réécrire à l’aide d’un radical. Dans le tableau ci-dessus, remarquez comment le dénominateur de l’exposant rationnel détermine l’indice de la racine. Ainsi, un exposant de ![]() se traduit par la racine carrée, un exposant de
se traduit par la racine carrée, un exposant de ![]() se traduit par la cinquième racine ou
se traduit par la cinquième racine ou ![]() , et
, et ![]() se traduit par la huitième racine ou
se traduit par la huitième racine ou ![]() .
.
|
Example |
||
|
Problem |
Write |
|
|
|
The radical form |
|
|
Answer |
|
|
|
Example |
||
|
Problem |
Express |
|
|
|
Réécrivez l’expression avec l’exposant fractionnaire comme radical. Le dénominateur de la fraction détermine la racine, dans ce cas la racine cubique. Les parenthèses de |
|
|
Réponse |
|
|
Rappelez-vous que les exposants ne font référence qu’à la quantité immédiatement à leur gauche, sauf si un symbole de regroupement est utilisé. L’exemple ci-dessous ressemble beaucoup à l’exemple précédent avec une différence importante — il n’y a pas de parenthèses! Regarde ce qui se passe.
|
Example |
||
|
Problem |
Express |
|
|
|
Rewrite the expression with the fractional exponent as a radical. Le dénominateur de la fraction détermine la racine, dans ce cas la racine cubique. L’exposant se réfère uniquement à la partie de l’expression immédiatement à gauche de l’exposant, dans ce cas x, mais pas le 2. |
|
|
Answer |
|
|
Rewriting Expressions with Rational Exponents Using Radicals
Just as you can rewrite an expression with a rational exponent as a radical expression, you can express a radical expression using a rational exponent.
|
Example |
||
|
Problem |
Express |
|
|
|
Rewrite the radical using a rational exponent. The root determines the fraction. Dans ce cas, l’indice du radical est 3, donc l’exposant rationnel sera Comme 4 est en dehors du radical, il n’est pas inclus dans le symbole de regroupement et l’exposant ne s’y réfère pas. |
|
|
Answer |
|
|
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the expression with the fractional exponent as a radical. |
|
|
6 • x2 |
Find the square root of both the coefficient and the variable. |
|
|
Réponse |
|
|
Exposants rationnels avec des numérateurs Autres qu’Un
Tous les les numérateurs pour les exposants fractionnaires dans les exemples ci-dessus étaient 1. Vous pouvez utiliser des exposants fractionnaires qui ont des numérateurs autres que 1 pour exprimer des racines, comme indiqué ci-dessous. Remarquez des motifs dans ce tableau?
|
Radical |
Exponent |
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
… |
|
|
|
Pour réécrire un radical en utilisant un exposant fractionnaire, la puissance à laquelle le radicand est élevé devient le numérateur et la racine devient le dénominateur.
Écriture d’exposants fractionnaires
Tout radical sous la forme ![]() peut être écrit en utilisant un exposant fractionnaire sous la forme
peut être écrit en utilisant un exposant fractionnaire sous la forme ![]() .
.
La relation entre ![]() et
et ![]() fonctionne également pour les exposants rationnels qui ont un numérateur de 1. Par exemple, le radical
fonctionne également pour les exposants rationnels qui ont un numérateur de 1. Par exemple, le radical ![]() peut également être écrit comme
peut également être écrit comme ![]() , car tout nombre reste la même valeur s’il est élevé à la première puissance. Vous pouvez maintenant voir d’où vient le numérateur de 1 sous la forme équivalente de
, car tout nombre reste la même valeur s’il est élevé à la première puissance. Vous pouvez maintenant voir d’où vient le numérateur de 1 sous la forme équivalente de ![]() .
.
Simplifier les expressions radicales En utilisant des Exposants Rationnels et les Lois des Exposants
Explorons maintenant certaines expressions radicales et voyons comment les simplifier. Voici une expression radicale qui doit être simplifiée, ![]() .
.
Une méthode de simplification de cette expression consiste à factoriser et à extraire des groupes de a3, comme indiqué ci-dessous dans cet exemple.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite by factoring out cubes. |
|
|
|
Write each factor under its own radical and simplify. |
|
|
Réponse |
|
|
Vous pouvez également simplifier cette expression en considérant le radical comme une expression avec un exposant rationnel, et en utilisant le principe que tout radical sous la forme ![]() peut être écrit en utilisant un exposant fractionnaire sous la forme
peut être écrit en utilisant un exposant fractionnaire sous la forme ![]() .
.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the radical using a rational exponent. |
|
|
|
Simplify the exponent. |
|
|
Answer |
|
|
Note that rational exponents are subject to all of the same rules as other exponents when they appear in algebraic expressions.
Les deux méthodes de simplification ont donné le même résultat, a2. Selon le contexte du problème, il peut être plus facile d’utiliser une méthode ou l’autre, mais pour l’instant, vous remarquerez que vous avez pu simplifier cette expression plus rapidement en utilisant des exposants rationnels que lors de l’utilisation de la méthode « pull-out”.
Essayons un autre exemple.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the radical using rational exponents. Use the rules of exponents to simplify the expression. |
|
|
|
||
|
|
Change the expression with the exposant rationnel de retour à la forme radicale. |
|
|
Réponse |
|
|
Encore une fois, la méthode alternative consiste à travailler sur la simplification sous le radical en utilisant l’affacturage. Pour l’exemple que vous venez de résoudre, cela ressemble à ceci.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the expression. |
|
|
|
Factor each radicand. |
|
|
|
Simplify. |
|
|
Answer |
|
|
Which of the expressions below is equal to the expression ![]() when written using a rational exponent?
when written using a rational exponent?
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Essayons une expression plus compliquée, ![]() . Cette expression a deux variables, une fraction et un radical. Prenons-le étape par étape et voyons si l’utilisation d’exposants fractionnaires peut nous aider à le simplifier.
. Cette expression a deux variables, une fraction et un radical. Prenons-le étape par étape et voyons si l’utilisation d’exposants fractionnaires peut nous aider à le simplifier.
Commençons par simplifier le dénominateur, car c’est là que se trouve le signe radical.
|
Example |
|||
|
Problem |
Simplify. |
||
|
|
Separate the factors in the denominator. |
||
|
|
Take the cube root of 8, which is 2. |
||
|
|
|
Rewrite the radical using a fractional exponent. |
|
|
|
Rewrite the fraction as a series of factors in order to cancel factors (see next step). |
||
|
|
Simplify the constant and c factors. |
||
|
|
Use the rule of negative exponents, n-x= |
||
|
|
Combine the b factors by adding the exponents. |
||
|
|
Change the expression with the fractional exponent back to radical form. Par convention, une expression n’est généralement pas considérée comme simplifiée si elle a un exposant fractionnaire ou un radical dans le dénominateur. |
||
|
Réponse |
|
||
Eh bien, cela a pris un certain temps, mais vous l’avez fait. Vous avez appliqué ce que vous savez sur les exposants fractionnaires, les exposants négatifs et les règles des exposants pour simplifier l’expression.
Résumé
Un radical peut être exprimé comme une expression avec un exposant fractionnaire en suivant la convention ![]() . La réécriture des radicaux à l’aide d’exposants fractionnaires peut être utile pour simplifier certaines expressions radicales. Lorsque vous travaillez avec des exposants fractionnaires, n’oubliez pas que les exposants fractionnaires sont soumis à toutes les mêmes règles que les autres exposants lorsqu’ils apparaissent dans des expressions algébriques.
. La réécriture des radicaux à l’aide d’exposants fractionnaires peut être utile pour simplifier certaines expressions radicales. Lorsque vous travaillez avec des exposants fractionnaires, n’oubliez pas que les exposants fractionnaires sont soumis à toutes les mêmes règles que les autres exposants lorsqu’ils apparaissent dans des expressions algébriques.
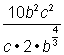
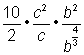
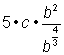
Leave a Reply