Le graphique d’une inégalité linéaire dans une variable est une ligne numérique. Utilisez un cercle ouvert pour < et > et un cercle fermé pour ≤ et ≥.

Le graphique pour x >-3

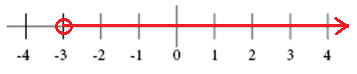
Le graphique pour x ≥ 2

Les inégalités qui ont les mêmes solutions sont appelées équivalentes. Il y a des propriétés d’inégalités ainsi que des propriétés d’égalité. Toutes les propriétés ci-dessous sont également valables pour les inégalités impliquant ≥ et ≤.

La propriété d’addition de l’inégalité indique que l’ajout du même nombre de chaque côté de l’inégalité produit une inégalité équivalente

IfIf\:x > y, \:then\:x +z >y +z

If If\:x <y, \: puis\: x + z < y + z$$

La propriété de soustraction de l’inégalité nous indique que la soustraction du même nombre des deux côtés d’une inégalité donne une inégalité équivalente.

IfIf\:x > y, \:puis \:x-z > y-z$$

If If\:x < y, \: alors\:x-z <y-z$$

La propriété de multiplication de l’inégalité nous indique que la multiplication des deux côtés d’une inégalité avec un nombre positif produit une inégalité équivalente.

IfIf\:x >y\: et\: z>0,\: alors\: xz>yz$$

$$Si\: x<y\: et\: z>0,\: alors\: xz<yz$$

la Multiplication de chaque côté d’une inégalité par un nombre négatif de l’autre main pour ne pas produire un équivalent à l’inégalité, à moins que nous aussi inverser le sens de l’inégalité

$$Si \: x>y \: et\: z<0,\: alors\: xz<yz$$

$$Si\: x<y\: et\: z < 0, \:then\:xz >yz$$

Il en va de même pour la propriété de division de l’inégalité.

La division des deux côtés d’une inégalité avec un nombre positif produit une inégalité équivalente.

IfIf\:x >y\: et \:z > 0, \: puis \:\frac{x}{z} >\frac{y}{z}$$

If If\:x

y\: et \:z > 0, \: puis\: \frac{x}{z}< \frac{y}{z}$$

Et la division des deux côtés d’une inégalité avec un nombre négatif produit une inégalité équivalente si le symbole d’inégalité est inversé.

IfIf\:x >y\: et \:z < 0, \: puis \:\frac{x}{z} <\frac{y}{z}$$

If If\:x < y \: et \:z < 0, \:then \:\frac{x}{z} > \frac{y}{z}$$

Pour résoudre une inégalité en plusieurs étapes, vous faites comme vous l’avez fait lors de la résolution d’équations en plusieurs étapes. Prenez une chose à la fois en commençant de préférence par isoler la variable des constantes. Lors de la résolution des inégalités en plusieurs étapes, il est important de ne pas oublier d’inverser le signe d’inégalité lors de la multiplication ou de la division par des nombres négatifs.

Exemple

Résoudre l’inégalité

$$-2\left(x+3\right) <10$$