J’ai toujours confondu « permutation » et ”combinaison » — laquelle est laquelle?

Voici un moyen facile de se souvenir: la permutation semble compliquée, n’est-ce pas? Et ça l’est. Avec les permutations, chaque petit détail compte. Alice, Bob et Charlie est différent de Charlie, Bob et Alice (insérez les noms de vos amis ici).

Les combinaisons, en revanche, sont assez faciles à vivre. Les détails n’ont pas d’importance. Alice, Bob et Charlie est le même que Charlie, Bob et Alice.

Les permutations sont pour les listes (l’ordre compte) et les combinaisons sont pour les groupes (l’ordre n’a pas d’importance).

Vous savez, un « verrou à combinaison » devrait vraiment s’appeler un « verrou à permutation ». L’ordre dans lequel vous mettez les chiffres compte.

Un vrai « verrou à combinaison » accepterait à la fois 10-17-23 et 23-17-10 comme corrects.

Permutations: Les détails poilus

Commençons par les permutations, ou toutes les façons possibles de faire quelque chose. Nous utilisons le terme de « permutation », nous allons donc nous soucier de chaque détail, y compris de l’ordre de chaque article. Disons que nous avons 8 personnes:

1: Alice2: Bob3: Charlie4: David5: Eve6: Frank7: George8: Horatio

De combien de façons pouvons-nous attribuer un 1er, 2e et 3e prix parmi huit candidats? (Or / Argent / Bronze)

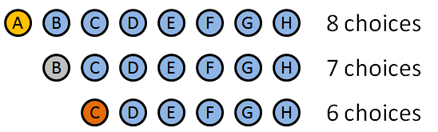
Nous allons utiliser des permutations car l’ordre dans lequel nous distribuons ces médailles compte. Voici comment ça se décompose:

• Médaille d’or: 8 choix: A B C D E F G H (Intelligent comment j’ai fait correspondre les noms avec des lettres, hein?). Disons que A gagne l’or.
• Médaille d’argent: 7 choix: B C D E F G H. Disons que B remporte l’argent.
• Médaille de bronze: 6 choix: C D E F G H. Disons que… C remporte le bronze.

Nous avons choisi certaines personnes pour gagner, mais les détails n’ont pas d’importance: nous avions 8 choix au début, puis 7, puis 6. Le nombre total d’options était de $8 * 7 * 6 = 336$.

Regardons les détails. Nous avons dû commander 3 personnes sur 8. Pour ce faire, nous avons commencé avec toutes les options (8) puis les avons enlevées une à la fois (7, puis 6) jusqu’à ce que nous manquions de médailles.

Nous savons que la factorielle est:

Malheureusement, cela en fait trop! Nous voulons seulement $8 * 7 * 6$. Comment peut-on ”arrêter » la factorielle à 5 ?

C’est là que les permutations deviennent cool: remarquez comment nous voulons nous débarrasser de $5 * 4 * 3 * 2 * 1$. Quel autre nom pour ça? 5 factorielle!

Donc, si nous faisons 8!/5! nous obtenons:

Et pourquoi avons-nous utilisé le nombre 5? Parce qu’il en restait après avoir pris 3 médailles sur 8. Donc, une meilleure façon d’écrire ceci serait :

où 8!/(8-3)! est juste une façon élégante de dire « Utilisez les 3 premiers nombres de 8!”. Si nous avons n éléments au total et que nous voulons choisir k dans un certain ordre, nous obtenons :

Et voici la formule de permutation de fantaisie: Vous avez n articles et vous voulez trouver le nombre de façons de commander k articles:

Combinaisons, Ho!

Les combinaisons sont faciles à vivre. L’ordre n’a pas d’importance. Vous pouvez le mélanger et il a la même apparence. Disons que je suis un bon marché et que je ne peux pas me permettre des médailles d’or, d’argent et de bronze séparées. En fait, je ne peux me permettre que des boîtes de conserve vides.

Combien de façons puis-je donner 3 boîtes de conserve à 8 personnes?

Eh bien, dans ce cas, l’ordre dans lequel nous choisissons les gens n’a pas d’importance. Si je donne une boîte à Alice, Bob et ensuite Charlie, c’est la même chose que de donner à Charlie, Alice et ensuite Bob. De toute façon, ils sont tout aussi déçus.

Cela soulève un point intéressant — nous avons quelques redondances ici. Alice Bob Charlie = Charlie Bob Alice. Un instant, voyons de combien de façons nous pouvons réorganiser 3 personnes.

Eh bien, nous avons 3 choix pour la première personne, 2 pour la seconde et seulement 1 pour la dernière. Nous avons donc $3 * 2 * 1 ways façons de réorganiser 3 personnes.

Attendez une minute this cela ressemble un peu à une permutation! Tu m’as trompé!

En effet, je l’ai fait. Si vous avez N personnes et que vous voulez savoir combien d’arrangements il y a pour toutes, c’est juste N factoriel ou N!

Donc, si nous avons 3 boîtes de conserve à donner, il y en a 3 ! ou 6 variantes pour chaque choix que nous choisissons. Si nous voulons savoir combien de combinaisons nous avons, nous créons simplement toutes les permutations et divisons par toutes les redondances. Dans notre cas, nous obtenons 336 permutations (d’en haut), et nous divisons par les 6 redondances pour chaque permutation et obtenons 336/6 = 56.

La formule générale est

ce qui signifie « Trouvez toutes les façons de choisir k personnes parmi n, et divisez par le k! variantes”. En écrivant cela, nous obtenons notre formule de combinaison, ou le nombre de façons de combiner k éléments d’un ensemble de n:

Parfois C(n, k) s’écrit comme suit:

qui est le coefficient binomial.

Quelques exemples

Voici quelques exemples de combinaisons (l’ordre n’a pas d’importance) à partir de permutations (l’ordre compte).

• Combinaison : Choisir une équipe de 3 personnes parmi un groupe de 10. CC (10,3) = 10!/(7! * 3!) = 10 * 9 * 8 / (3 * 2 * 1) = 120$.

  Permutation: Choisir un président, un vice-président et un Waterboy parmi un groupe de 10. PP (10,3) = 10 !/7! = 10 * 9 * 8 = 720$.

• Combinaison : Choisir 3 desserts dans un menu de 10. C (10,3) = 120.

  Permutation : Lister vos 3 desserts préférés, dans l’ordre, à partir d’un menu de 10. P(10,3) = 720.

Ne mémorisez pas les formules, comprenez pourquoi elles fonctionnent. Les combinaisons semblent plus simples que les permutations, et elles le sont. Vous avez moins de combinaisons que de permutations.

Autres Articles De Cette Série

1. Permutations et Combinaisons Faciles
2. Naviguez Dans une Grille À L’Aide De Combinaisons Et De Permutations
3. Comment Comprendre Les Combinaisons À L’Aide De La Multiplication
4. Pourquoi multiplions-nous les combinaisons?