Nombres complexes: Introduction (page 1 sur 3)

Sections: Introduction, Opérations avec des complexes, La Formule quadratique

Jusqu’à présent, on vous a dit que vous ne pouvez pas prendre la racine carrée d’un nombre négatif. C’est parce que vous n’aviez pas de nombres négatifs après les avoir carrés (vous ne pouviez donc pas « reculer » en prenant la racine carrée). Chaque nombre était positif après l’avoir quadrillé. Donc, vous ne pouviez pas très bien enraciner un négatif et vous attendre à trouver quelque chose de sensé.

Maintenant, cependant, vous pouvez prendre la racine carrée d’un nombre négatif, mais cela implique d’utiliser un nouveau nombre pour le faire. Ce nouveau nombre a été inventé (découvert?) à l’époque de la Réforme. À cette époque, personne ne croyait qu’une utilisation « réelle » serait trouvée pour ce nouveau nombre, à part faciliter les calculs impliqués dans la résolution de certaines équations, de sorte que le nouveau nombre était considéré comme un nombre fictif inventé pour des raisons de commodité.

(Mais alors, quand on y pense, tous les nombres ne sont-ils pas des inventions? Ce n’est pas comme si les nombres poussaient sur les arbres! Ils vivent dans nos têtes. On les a tous inventés ! Pourquoi ne pas en inventer un nouveau, tant que cela fonctionne bien avec ce que nous avons déjà?)

Alors:

Maintenant, vous pouvez penser que vous pouvez le faire:

Mais cela n’a aucun sens! Vous avez déjà deux nombres carrés à 1; à savoir -1 et +1. Et j’ai déjà des carrés à -1. Il n’est donc pas raisonnable que je me place également à 1. Cela souligne un détail important: Lorsque vous traitez avec des imaginaires, vous gagnez quelque chose (la capacité de traiter les négatifs à l’intérieur des racines carrées), mais vous perdez également quelque chose (une partie de la flexibilité et des règles pratiques que vous aviez auparavant lorsque vous traitiez avec des racines carrées). En particulier, VOUS DEVEZ TOUJOURS FAIRE LA PARTIE i EN PREMIER!

• Simplifiez sqrt(-9). Copyright © Elizabeth Stapel 2000-2011 Tous droits réservés

(Attention: L’étape qui passe par le troisième signe « égal » est « « , pas « « . Le je est en dehors du radical.)

• Simplifiez sqrt(-25).

• Simplifiez sqrt(-18).

• Simplify–sqrt(-6).

Dans vos calculs, vous traiterez i comme vous le feriez avec x, à l’exception du fait que x2 est juste x2, mais i2 est -1:

• Simplifiez 2i + 3i.

2i +3i =(2 +3)i =5i

• Simplifiez 16i–5i.

16i–5i =(16–5) i= 11i

• Multiplier et simplifier (3i)(4i).

(3i)(4i) =(3·4)(i*i) =(12)(i2) = (12)(-1) = -12

• Multiplier et simplifier (i)(2i)(-3i).

(i)(2i)(–3i) =(2·-3)(i·i·i) =(-6)(i2·i)

=(-6)(-1·i) =(-6)(–i) =6i

Notez ce dernier problème. En son sein, vous pouvez voir que , car i2 =-1. En continuant, nous obtenons:

Ce modèle de puissances, de signes, de 1 et de i est un cycle:

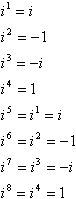
En d’autres termes, pour calculer toute puissance élevée de i, vous pouvez la convertir en une puissance inférieure par prendre le multiple le plus proche de 4 qui n’est pas plus grand que l’exposant et soustraire ce multiple de l’exposant. Par exemple, une question d’astuce courante sur les tests est quelque chose du genre « Simplifiez i99 », l’idée étant que vous essaierez de multiplier i quatre-vingt-dix-neuf fois et que vous manquerez de temps, et les enseignants auront un bon rire à vos frais dans le salon de la faculté. Voici comment fonctionne le raccourci:

i99 = i96 + 3= i(4×24) +3= i3=–i

C’est-à-dire i99 = i3, car vous pouvez simplement supprimer l’i96. (Quatre-vingt-seize est un multiple de quatre, donc i96 est juste 1, que vous pouvez ignorer.) En d’autres termes, vous pouvez diviser l’exposant par 4 (en utilisant la division longue), jeter la réponse et n’utiliser que le reste. Cela vous donnera la partie de l’exposant qui vous tient à cœur. Voici quelques autres exemples :

• Simplifiez i17.

i17= i16 +1= i4·4 +1=i1=i

• Simplifiez i120.

i120= i4 ·30= i4 ·30 +0=i0=1

• Simplifier i64,002.

i64,002 = i64,000 + 2 = i4 · 16,000 + 2 = i2 = –1

Top | 1 | 2 | 3 | Return to Index Next >>