Magazine beanz
Carte de Merian-Erben (1652) sur Wikipedia
Le casse-tête mathématique de ce mois-ci remonte à 1735, date à laquelle il a été résolu pour la première fois par Leonhard Euler, mathématicien et physicien suisse.
Le puzzle s’appelle Les Sept Ponts de Königsberg. Il est basé sur une ville réelle, alors en Prusse, maintenant Kaliningrad en Russie. La ville est divisée par une rivière avec deux îles entre les deux et, plus en aval, la rivière divise à nouveau la ville.
Le problème est trompeusement simple: il y a (ou était, à l’époque d’Euler) sept ponts pour relier les deux îles et les parties aval de la ville. Euler se demandait si une personne pouvait traverser chacun des sept ponts une fois et une seule fois pour toucher chaque partie de la ville. Commencer et se terminer au même endroit n’était pas une exigence.
Voici une carte que vous pouvez utiliser pour essayer de résoudre le problème par vous-même:
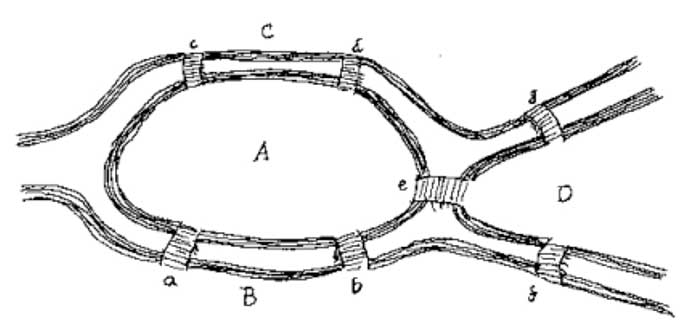
Qui pensez-vous que c’est plus important pour résoudre ce problème: le nombre de ponts ou l’emplacement de chaque pont?
Réponse : le nombre de ponts.
Euler a prouvé que le nombre de ponts doit être un nombre pair, par exemple, six ponts au lieu de sept, si vous voulez traverser chaque pont une fois et vous rendre dans chaque partie de Königsberg. La solution considère chaque pont comme un point final, un sommet en termes mathématiques et les connexions entre chaque pont (sommet). Euler réalisa que seul un nombre pair de ponts donnait le résultat correct de pouvoir toucher chaque partie de la ville sans traverser un pont deux fois.
Euler a utilisé les mathématiques pour prouver qu’il était impossible de traverser les sept ponts une seule fois et de visiter chaque partie de Königsberg. Ce faisant, il a mis en mouvement une série de découvertes et d’idées sur la façon dont l’espace et les espaces qui se croisent peuvent être définis, ainsi que leurs propriétés. Une description détaillée de la solution d’Euler dans le lien Wikipedia ci-dessous cet article.
Si vous avez déjà vu une bande de mobius, par exemple, vous avez vu un exemple de topologie, un domaine d’étude mathématique a évolué à partir de la solution d’Euler à ce problème. La topologie concerne l’espace et la façon dont les choses se connectent les unes aux autres, ainsi que la continuité et les limites de l’espace. La topologie étudie également comment les propriétés d’un espace changent et ne changent pas lorsque l’espace est agrandi ou contracté.
En informatique, la topologie est utile pour comprendre les réseaux (chemins) que les données peuvent circuler dans n’importe quel système, ainsi que la façon dont les ensembles de données peuvent se relier les uns aux autres. Les Sept Ponts de Königsberg sont également similaires à un autre problème informatique courant appelé parfois le Problème du Vendeur itinérant où vous essayez de trouver l’itinéraire le plus efficace compte tenu d’un ensemble de restrictions comme les sept ponts dans le problème d’Euler.
Les non-mathématiciens (probablement vous, certainement moi) éprouvent le problème du vendeur itinérant chaque fois que nous montons dans un train ou un bus. Le problème du vendeur itinérant consiste à trouver le moyen le plus efficace de voyager entre des paires de villes de distances spécifiées. La gestion des ressources rares (trains, bus) qui circulent sur des itinéraires finis est un problème parfait pour l’informatique car les ordinateurs sont plus rapides et plus efficaces. Mais d’abord, nous avons besoin d’Euler et d’autres pour énoncer le problème et définir des solutions avec les mathématiques. Nous programmons ensuite nos ordinateurs pour faire le calcul.
La topologie traite également de la théorie des ensembles, de la façon dont des groupes de choses peuvent être triés en ensembles pour identifier des éléments communs avec d’autres groupes ainsi que des éléments uniques. Un diagramme de Venn est un excellent exemple d’ensemble. Et la programmation doit parfois trier les données de différentes manières. La méthode de tri qui fonctionne le mieux pour une situation peut être déterminée par la théorie des ensembles.
Et qu’est-il arrivé aux sept ponts du temps d’Euler ? Deux ponts ont été démolis et remplacés par une seule autoroute. Des trois ponts restants, l’un a été reconstruit en 1935 tandis que les deux autres restent intacts tels qu’Euler les connaissait. Et, bien sûr, Königsberg, la Prusse a changé de nom pour Kaliningrad, en Russie.
Leave a Reply