Les mathématiques sont plus un marathon qu’un sprint — c’est une mouture longue, lente et régulière, avec de rares moments de percée. Pourtant, de temps en temps, nous obtenons ces précieux moments « Eurêka”, ces courtes lignes de lettres et de chiffres qui changent la science pour toujours. Voici quelques-unes des équations les plus célèbres, des anciens Grecs à la physique moderne.

Théorème de Pythagore (530 av.J.-c.)

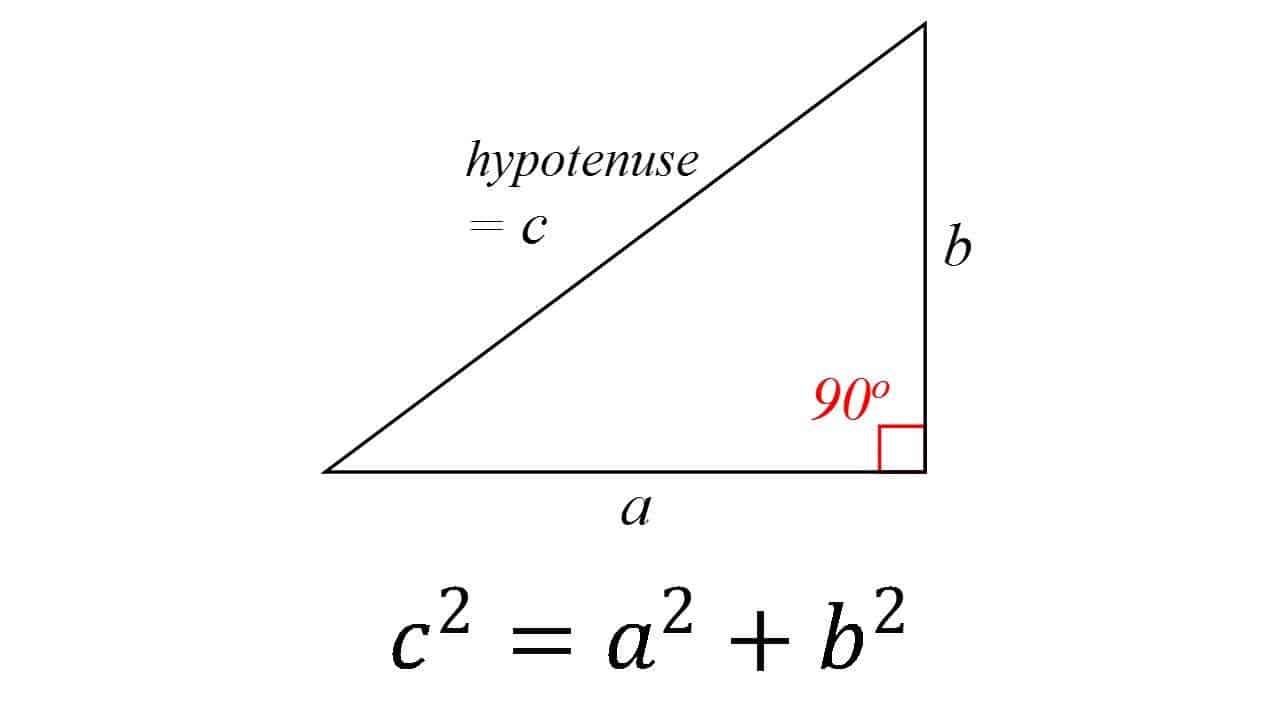
C’est l’un des piliers fondateurs de toute la géométrie: dans un triangle rectangle, le carré de l’hypoténuse (le côté opposé à l’angle droit) est égal à la somme des carrés des deux autres. La théorie est généralement attribuée au mathématicien grec Pythagore, bien qu’il existe des preuves que les mathématiciens babyloniens ont compris la formule. Il est également très possible que le théorème soit connu de nombreuses personnes, mais il a été le premier à le prouver.

Le théorème a reçu de nombreuses preuves – peut-être la plus pour tout théorème mathématique. Ils sont très divers, y compris les preuves géométriques et les preuves algébriques, certaines remontant à des milliers d’années.

Nombres complexes

Le mathématicien italien Gerolamo Cardano est le premier connu à avoir introduit des nombres complexes, les qualifiant de « fictifs” à l’époque. Cependant, le développement mathématique de « i” en tant que nombre imaginaire représentant la racine carrée de -1 est attribué à Leonhard Euler, l’un des mathématiciens et scientifiques les plus importants de l’histoire humaine.

Les nombres complexes sont essentiellement des nombres qui n’existent pas vraiment, mais qui sont très utiles pour un certain nombre de calculs. Ils se composent de nombres avec une partie réelle (les nombres que nous connaissons tous) et une partie imaginaire (le i représenté ici) et ont des applications pratiques dans de nombreux domaines, y compris la physique, la chimie, la biologie, l’économie, le génie électrique et les statistiques.

Les logarithmes

Les logarithmes sont fondamentalement la fonction inverse de l’exponentiation. Vous avez besoin d’un nombre (N), d’une base (a), et le logarithme de N dans la base a sera x, où N est égal à a à la puissance de x. Cela peut sembler une manière différente d’écrire la même chose (et dans un sens, c’est le cas), mais les logarithmes ont une myriade d’applications pratiques, utilisées en psychologie, en économie et pour mesurer de nombreux phénomènes physiques (tels que le pH ou la magnitude d’un tremblement de terre).

Les logarithmes ont été publiquement proposés par John Napier en 1614, dans un livre intitulé Mirifici Logarithmorum Canonis Descriptio (Description de la Merveilleuse Règle des Logarithmes) — un titre approprié. Un cas particulier de logarithme est le logarithme naturel -e, où e est un nombre irrationnel et transcendantal approximativement égal à 2,71828182845. En fait, e lui-même a une histoire fascinante et un nombre impressionnant d’applications, mais c’est une histoire pour une autre fois.

Calcul

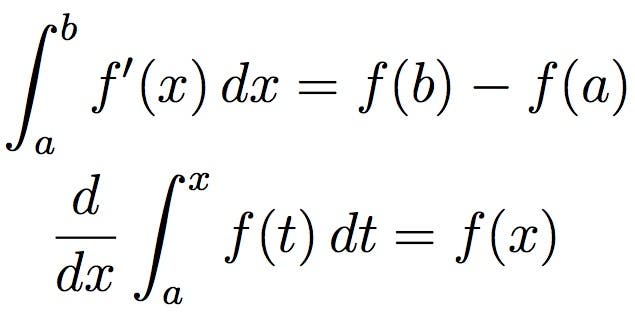
Peu de domaines des mathématiques ont eu autant d’impact que le calcul. Développé au 17ème siècle par Isaac Newton et Gottfried Wilhelm Leibniz, le calcul est largement utilisé en science, en ingénierie et en économie. Le calcul se concentre généralement sur le traitement de petites quantités, en particulier des quantités infiniment petites. Grâce au calcul, ceux-ci peuvent être traités comme des nombres réels, même s’ils sont techniquement infiniment petits.

Pour une visualisation plus simple, l’intégration, représentée ci-dessus, peut être considérée comme la mesure de l’aire sous une courbe, définie par une fonction.

La Loi de la Gravité

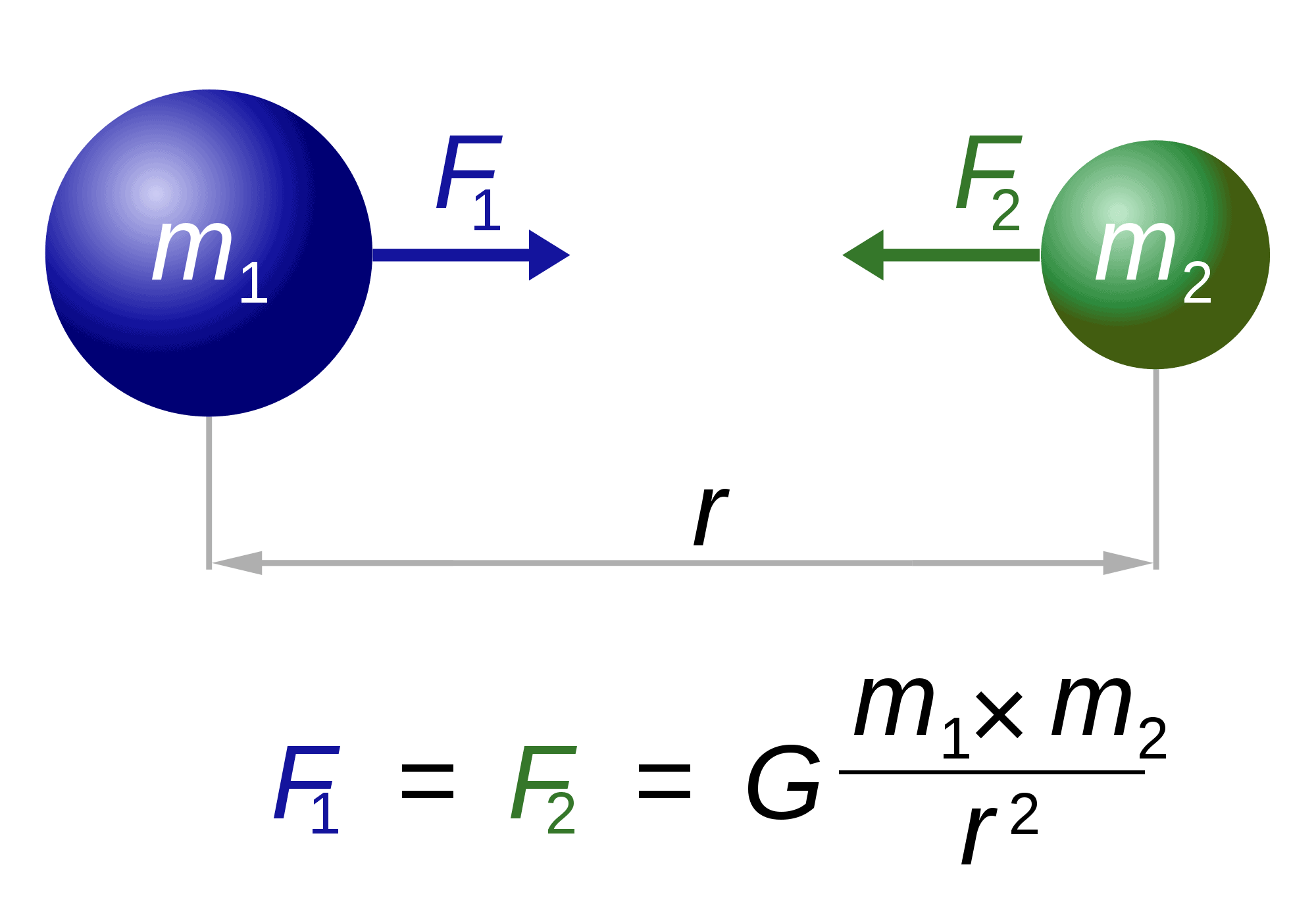
En parlant de Newton, il est également ”responsable » de l’une des équations les plus célèbres et spectaculaires au monde: la loi de la gravité.

La loi décrit essentiellement comment deux corps quelconques de masses m1 et m2 sont attirés l’un par l’autre. La force (F1, F2) est inversement proportionnelle au carré de la distance qui les sépare (r). Le seul facteur restant, G, est une constante gravitationnelle. La nature de cette constante reste insaisissable.

Relativité générale

Pendant près de 200 ans, la loi de Newton a défini notre niveau de compréhension de la mécanique. Le travail d’Einstein au 20ème siècle a fait passer les choses au niveau supérieur — ces deux réalisations se dressent sur les plus hauts socles du monde de la physique.

La relativité générale est essentiellement une théorie géométrique de la gravitation, généralisant la théorie de Newton fournissant une description unifiée de la gravité en tant que propriété géométrique de l’espace et du temps — ou de l’espace-temps. En particulier, Einstein a montré non seulement qu’il existe une chose telle que « l’espace-temps” fusionnant les trois dimensions avec la 4ème dimension du temps, mais il a également montré que cet espace-temps peut être courbé par gravité, la courbure étant directement liée à l’énergie et à l’élan de la matière et du rayonnement présents.

Deuxième loi de la thermodynamique

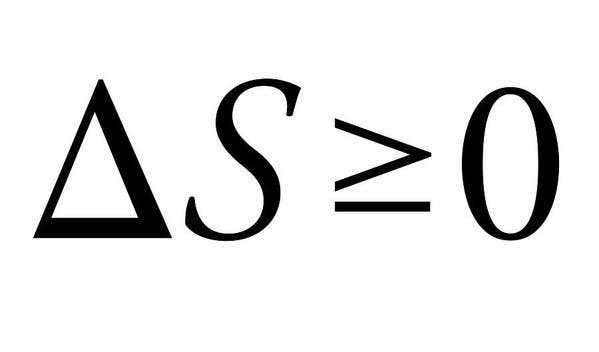
La Deuxième Loi de la thermodynamique explique pourquoi nous ne pouvons pas avoir de belles choses dans l’Univers. Les quatre lois de la thermodynamique définissent les grandeurs physiques fondamentales (température, énergie et entropie) qui caractérisent les systèmes thermodynamiques. Le second, en particulier, se distingue ici par sa simplicité, mais ses implications absolument massives.

La loi stipule essentiellement que la somme des entropies des systèmes thermodynamiques en interaction doit toujours augmenter, ou tout au plus rester constante. Lorsque l’énergie change d’une forme à l’autre ou que la matière se déplace, l’entropie (ou le désordre) dans un système fermé augmente. Toutes les différences de température, de pression et de densité ont tendance à s’aplatir après un certain temps

Les équations de Maxwell

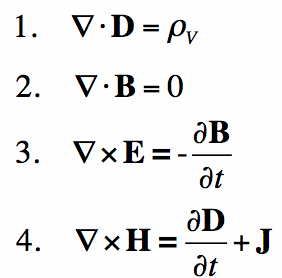
En termes simples, les équations de Maxwell sont à l’électromagnétisme ce que la loi de Newton est à la mécanique. Ils fournissent une base mathématique pour l’électromagnétisme classique, l’optique classique et les circuits électriques. Ils sont largement utilisés dans l’appareil même sur lequel vous lisez ceci — en gros, tous les appareils électroniques.

Les lois de Maxwell décrivent comment les champs électriques et magnétiques sont générés par les charges, les courants et les changements des champs. Une percée significative a été la démonstration que les champs électriques et magnétiques se propagent à la vitesse de la lumière.

Identité d’Euler

Enfin, c’est probablement l’équation la plus élégante, d’une beauté suprême, car elle implique tous les nombres « de base” :

• 0, qui est neutre pour l’addition et la soustraction;
• 1, qui est neutre pour la multiplication et la division;
• e, qui est le nombre d’Euler (voir ci-dessus), la base des logarithmes naturels;
• i est l’unité imaginaire (voir ci-dessus); et
• π est pi, le rapport de la circonférence d’un cercle à son diamètre.

Trouver une relation qui unifie tous ces nombres n’est rien de moins qu’à couper le souffle, et semble assez improbable. La démonstration n’est pas vraiment simple, mais vous pouvez la voir ici.

Il est tout à fait normal que Keith Devlin, professeur de mathématiques à l’Université de Stanford, ait décrit l’équation en disant que « comme un sonnet shakespearien qui capture l’essence même de l’amour, ou une peinture qui fait ressortir la beauté de la forme humaine qui est bien plus qu’une simple peau profonde, l’équation d’Euler atteint les profondeurs de l’existence”

Il n’est pas souvent que les mathématiques et la physique se résument à des équations simples et élégantes — mais quand elles le font, c’est tout un spectacle à voir.