Avec le succès au box-office du film « Interstellar », beaucoup de gens sont enthousiasmés par les perspectives des trous de ver comme moyen de transport interstellaire. Bien qu’il n’y ait actuellement aucune preuve que de tels objets exotiques existent dans la nature, il est possible qu’ils puissent être créés artificiellement, peut-être à partir de versions de la théorie des cordes de dimension supérieure et de l’ingénierie de la mousse spatio-temporelle fondamentale. La recherche sur les trous de ver est aujourd’hui un sujet passionnant avec des dizaines d’articles publiés chaque année dans des revues à comité de lecture, mais il convient de rappeler ses origines – et cela commence à partir d’un endroit surprenant.

En 1915, Albert Einstein a publié sa théorie générale de la relativité, sa description de la gravité qui définit parfaitement comment les objets s’attireront les uns les autres et affecteront l’espace et le temps qui les entourent. De nombreuses années plus tard, le physicien américain John Wheeler monnayait la phrase « l’espace dit à la matière comment se déplacer, et la matière dit à l’espace comment se courber”. Einstein a décrit la gravité comme une manifestation de la courbure spatio-temporelle. La relativité générale est une théorie des champs continus contrairement à la théorie des particules de la matière qui a conduit à la mécanique quantique.

Einstein a également participé au développement de la mécanique quantique, la théorie qui décrit les particules subatomiques. Mais il n’était pas entièrement satisfait de ses incertitudes inhérentes et de son caractère probabiliste. Ainsi, en 1935, il a travaillé avec Nathan Rosen pour produire une théorie des champs pour les électrons, en utilisant la relativité générale. Leur article était intitulé « Le problème des particules dans la Théorie générale de la Relativité”. Einstein et Rosen étudiaient la possibilité d’une théorie atomiste de la matière et de l’électricité qui, à l’exclusion des discontinuités (singularités) dans le domaine, n’utilisait aucune autre variable que la description (métrique) de la relativité générale et la théorie électromagnétique de Maxwell. L’une des conséquences a été que la particule chargée la plus élémentaire s’est avérée être une particule de masse nulle.

Au final, ce qu’ils ont produit était quelque chose d’assez original. Ils ont commencé avec les équations pour une distribution de masse à symétrie sphérique, déjà utilisées pour les trous noirs, et connue sous le nom de solution de Schwarzschild,

dsds^2= -\dfrac{1}{1-2m/r} dr^2-r^2(d\theta^2 +\sin^2\theta d\phi^2)+(1-2m/r) dt^2

où \(ds^2\) est la métrique et \(m= GM/c ^2\) avec les coordonnées sphériques \((r, \thêta, \phi)\) et le temps \(t\).

Ils ont effectué une transformation de coordonnées pour supprimer la région contenant la singularité de courbure, une discontinuité dans la courbure de l’espace impliquée par les trous noirs et des phénomènes similaires. La singularité à \(r = 2m\) a été supprimée par la transformation de coordonnées \(u^2 = r-2m\), résultant en une solution finale,

dsds^2 = -4 (u^2 + 2m) du^2-(u^2 + 2m)^2 d\Omega^2 +\dfrac{u^2}{u^2 + 2m}dt^2

où \(d\Omega^2 = d\thêta^2+\sin^ 2\thêta d\ phi^ 2\).

Cette solution était une représentation mathématique de l’espace physique par un espace de deux feuilles asymptotiquement plates reliées par un pont ou un trou de ver de Schwarzschild avec une « gorge ». Cela relie les deux feuilles et, par analogie, deux parties distinctes de l’univers réel en trois dimensions. La figure 1 montre l’espace autour du trou de ver, l’espace au-dessus et en dessous devenant plat sur les « bords » lorsque vous effectuez un zoom arrière à l’infini.

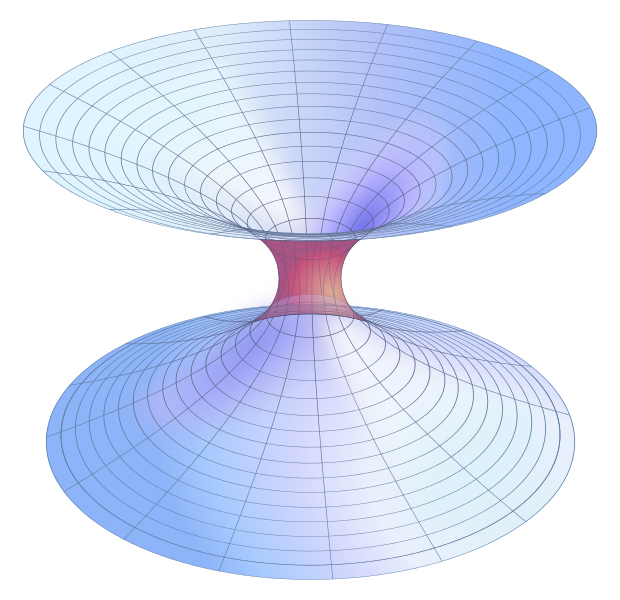
Ce n’était pas un trou de ver traversable, pour cela il fallait attendre l’arrivée des physiciens John Wheeler dans les années 1950 et Kip Thorne dans les années 1980. En 1987, avec l’encouragement de Carl Sagan pour son roman « Contact” (plus tard un long métrage), Thorne et son collègue Michael Morris ont pu construire une description mathématique, une métrique, pour décrire un trou de ver symétrique sphériquement et statique avec une circonférence réelle, finie. Cela avait une coordonnée diminuant de l’infini négatif dans un espace peu incurvé – à une valeur minimale où se trouvait la gorge, puis augmentant de la gorge à l’infini positif — dans un espace peu incurvé différent. Cette solution a la particularité de ne pas avoir d’horizon d’événements — contrairement à un trou noir. L’article de Thorne et Morris s’intitulait « Les trous de ver dans l’Espace-temps et leur utilisation pour le Voyage interstellaire: Un outil pour enseigner la Relativité Générale”. Cet article a contribué à faire de la recherche sur les trous de ver un nouveau domaine d’investigation académique.

Depuis, de nombreux articles ont été publiés, et en effet des relevés astronomiques ont été effectués, examinant les étoiles et les galaxies les plus éloignées à la recherche de trous de ver naturels. Aucun n’a encore été identifié, mais rappelez—vous l’origine de ce domaine de recherche – le pont Einstein-Rosen n’était pas un trou de ver traversable, et ce n’était pas l’intention de l’auteur d’en produire un, mais ils ont produit la première description mathématique d’un trou de ver. Ils devraient être rappelés pour cela. La recherche scientifique produit souvent quelque chose d’assez inattendu avec des implications allant bien au-delà des intentions initiales des chercheurs.

Kelvin D. Depuis la publication de cet article, notre magazine, Principium, a publié deux numéros (numéros 9&10) où nous discutons plus en détail des trous de ver et du pont Einstein-Rosen. Ces numéros détaillent également le symposium d’une journée sur « Les trous de ver Interstellaires: Physique et Réalisation pratique » organisé par l’Initiative pour les Études Interstellaires en collaboration avec la Société Interplanétaire britannique.