Évaluation du Kappa de Cohen

La valeur de kappa peut être inférieure à 0 (négative). Un score de 0 signifie qu’il y a un accord aléatoire entre les évaluateurs, alors qu’un score de 1 signifie qu’il y a un accord complet entre les évaluateurs. Par conséquent, un score inférieur à 0 signifie qu’il y a moins d’accord que de hasard. Ci-dessous, je vais vous montrer la formule pour résoudre ce problème, mais il est important que vous vous familiarisiez avec la figure 4 pour avoir une bonne compréhension.

La raison pour laquelle j’ai mis en évidence deux grilles deviendra claire dans un instant, mais pour l’instant, laissez-moi décomposer chaque grille.

A=>Le nombre total d’instances que les deux évaluateurs ont dites correctes. Les évaluateurs sont d’accord.

B= >Le nombre total d’instances que le évaluateur 2 a dit être incorrect, mais que le évaluateur 1 a dit être correct. C’est un désaccord.

C= >Le nombre total d’instances que le évaluateur 1 a déclaré être incorrect, mais que le évaluateur 2 a déclaré être correct. C’est aussi un désaccord.

D=> Le nombre total d’instances que les deux évaluateurs ont déclaré incorrectes. Les évaluateurs sont d’accord.

Pour calculer la valeur de kappa, nous devons d’abord connaître la probabilité d’accord (ceci explique pourquoi j’ai mis en évidence la diagonale d’accord). Cette formule est obtenue en additionnant le nombre de tests dans lesquels les évaluateurs sont d’accord, puis en le divisant par le nombre total de tests. En utilisant l’exemple de la figure 4, cela signifierait (A + D) / (A + B + C + D).

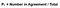
Parfait! L’étape suivante consiste à déterminer la probabilité d’accord aléatoire. En utilisant la figure 4 comme guide, la valeur attendue est le nombre total de fois que le Évaluateur 1 dit correct divisé par le nombre total d’instances, multiplié par le nombre total de fois que le Évaluateur 2 dit correct divisé par le nombre total d’instances, ajouté au nombre total de fois que le Évaluateur 1 dit incorrect multiplié par le nombre total de fois que le Évaluateur 2 dit incorrect. C’est beaucoup d’informations à prendre là-bas, donc dans la figure 6, j’ai formulé cette équation en utilisant la grille ci-dessus.

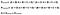
Lastly, the formula for Cohen’s Kappa is the probability of agreement take away the probability of random agreement divided by 1 minus the probability of random agreement.

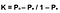
Super! Vous êtes maintenant en mesure de faire la distinction entre fiabilité et validité, d’expliquer le kappa de Cohen et de l’évaluer. Cette statistique est très utile, bien que depuis que j’ai compris comment cela fonctionne, je pense maintenant qu’elle peut être sous-utilisée lors de l’optimisation des algorithmes pour une métrique spécifique. De plus, le kappa de Cohen fait également un bon travail pour mesurer les problèmes de classe multi-classes et déséquilibrés.

P.s. S’il y a quelque chose que vous voulez que je couvre à propos de la science des données, vous pouvez m’envoyer un message direct sur Twitter @KurtisPykes ou laisser une réponse à ce message.