Intégrales définitives
Vous aimeriez peut-être d’abord lire Introduction à l’intégration!
Intégration
|
L’intégration peut être utilisée pour trouver des zones, des volumes, des points centraux et de nombreuses choses utiles. Mais il est souvent utilisé pour trouver l’aire sous le graphique d’une fonction comme celle-ci: |
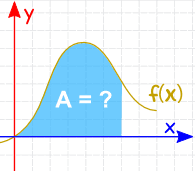 |
|
|
L’aire peut être trouvée en ajoutant des tranches qui approchent de zéro en largeur: Et il existe des règles d’intégration qui nous aident à obtenir la réponse. |
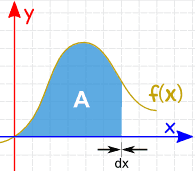 |
Notation

Le symbole pour « Integral » est un « S » élégant (pour « Sum », l’idée de sommer les tranches):
Après le Symbole Intégral, nous mettons la fonction dont nous voulons trouver l’intégrale (appelée Intégrande).
Puis terminez par dx pour signifier que les tranches vont dans la direction x (et approchent de zéro en largeur).
Intégrale définie
Une Intégrale Définie a des valeurs de début et de fin : en d’autres termes, il y a un intervalle.
a et b (appelés limites, limites ou limites) sont placés en bas et en haut du « S », comme ceci:
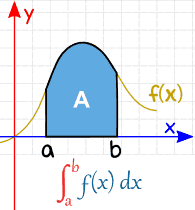 |
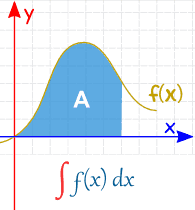 |
|
| Definite Integral (from a to b) |
Indefinite Integral (no specific values) |
We find the Definite Integral by calculating the Indefinite Integral at a, and at b, then subtracting:
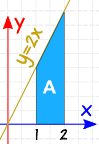
Exemple: Qu’est-ce que 2 ∫ 1 2x dx
On nous demande l’Intégrale Définie, de 1 à 2, de 2x dx
Nous devons d’abord trouver l’Intégrale Indéfinie .
En utilisant les Règles d’intégration, nous trouvons que ∫2x dx = x2 + C
Calculez maintenant cela à 1 et 2:
- À x = 1: ∫2x dx = 12 +C
- À x = 2: ∫2x dx = 22 +C
Soustraire:
Et « C » est annulé… donc, avec des intégrales définies, nous pouvons ignorer C.
Résultat:

Vérifier: avec une forme aussi simple, essayons également de calculer l’aire par géométrie:
A = 2+42 × 1 = 3
Oui, il a une superficie de 3.
(Oui!)
Notation: Nous pouvons montrer l’intégrale indéfinie (sans le +C) entre crochets, avec les limites a et b après, comme ceci:
Exemple (suite)
Un bon moyen de montrer votre réponse:
=
Essayons un autre exemple:
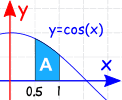
Example:
The Definite Integral, from 0.5 to 1.0, of cos(x) dx:
(Note: x must be in radians)
The Indefinite Integral is: ∫cos(x) dx = sin(x) + C
We can ignore C for definite integrals (as we saw above) and we get:
=
And another example to make an important point:
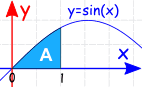
Example:
The Definite Integral, from 0 to 1, of sin(x) dx:
L’intégrale indéfinie est : ∫sin(x)dx=−cos(x ) +C
Puisque nous partons de 0, peut-on simplement calculer l’intégrale à x = 1 ?
– cos(1) = -0,540…
Quoi? C’est négatif ? Mais cela semble positif dans le graphique.
Eh bien… nous avons fait une erreur!
Parce qu’il faut soustraire l’intégrale à x= 0. Nous ne devrions pas supposer que c’est zéro.
Alors faisons-le correctement, en soustrayant l’un de l’autre:
=
C’est mieux !
Mais on peut avoir des régions négatives, lorsque la courbe est en dessous de l’axe :

Exemple:
L’Intégrale définie, de 1 à 3, de cos(x)dx :
Notez que certaines sont positives et d’autres négatives.
L’intégrale définie calculera la valeur nette.
Laissez-nous faire les calculs:
=
Saut il y a plus de négatif que de positif avec le résultat net de -0.700….
nous avons donc cette chose importante à retenir:
Essayez d’intégrer cos(x) avec différentes valeurs de début et de fin pour voir par vous-même comment fonctionnent les positifs et les négatifs.
Zone positive
Mais parfois, nous voulons que toute la zone soit traitée comme positive (sans que la partie en dessous de l’axe soit soustraite).
Dans ce cas, nous devons calculer les aires séparément, comme dans cet exemple:

Exemple: Quelle est l’aire totale entre y = cos(x) et l’axe des abscisses, de x = 1 à x = 3?
C’est comme l’exemple que nous venons de faire, mais maintenant nous nous attendons à ce que toute la zone soit positive (imaginez que nous devions la peindre).
Donc maintenant, nous devons faire les parties séparément:
- Une pour la zone au-dessus de l’axe des abscisses
- Une pour la zone en dessous de l’axe des abscisses
La courbe traverse l’axe des abscisses à x = π/2 donc nous avons:
De 1 à π /2:
div>
= sin(π/2) – sin(1)
De π/2 à 3:
= sin(3) − sin(π/2)
Ce dernier sort négatif, mais nous voulons qu’il soit positif, donc:
Surface totale = 0,159… + 0.859… = 1.018…
Ceci est très différent de la réponse de l’exemple précédent.
Continu
Oh oui, la fonction que nous intégrons doit être continue entre a et b : pas de trous, de sauts ou d’asymptotes verticales (où la fonction monte/descend vers l’infini).
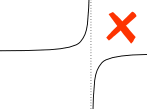
Exemple :
Une asymptote verticale entre a et b affecte l’intégrale définie.
Propriétés
Zone au−dessus – zone en dessous
L’intégrale ajoute la zone au-dessus de l’axe mais soustrait la zone en dessous, pour une « valeur nette »:
Ajout de fonctions
L’intégrale de f+g est égale à l’intégrale de f plus l’intégrale de g:
Inverser l’intervalle
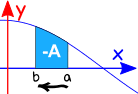
Inverser la direction de l’intervalle donne le négatif de la direction d’origine.
![]()
Leave a Reply