Gammes Interquartiles et Valeurs Aberrantes
Quartiles&Boxes5-Number Summariyiqrs&Valeurs aberrantes
Purplemath
La « plage interquartile », abrégée « IQR », est juste la largeur de la boîte dans le tracé en boîte et moustache. Autrement dit, IQR = Q3-Q1. L’IQR peut être utilisé comme mesure de l’étalement des valeurs.
Les statistiques supposent que vos valeurs sont regroupées autour d’une valeur centrale. L’IQR indique la répartition des valeurs « moyennes »; il peut également être utilisé pour indiquer quand certaines des autres valeurs sont « trop éloignées » de la valeur centrale. Ces points « trop éloignés » sont appelés « valeurs aberrantes », car ils « se situent en dehors » de la plage dans laquelle nous les attendons.
L’IQR est la longueur de la boîte dans votre parcelle de boîte et de moustache. Une valeur aberrante est toute valeur située à plus d’une fois et demie la longueur de la boîte à partir de chaque extrémité de la boîte.
Le contenu Continue Ci-Dessous
MathHelp.com
Autrement dit, si un point de données est inférieur à Q1 –1,5×IQR ou supérieur à Q3 + 1,5×IQR, il est considéré comme étant trop éloigné des valeurs centrales pour être raisonnable. Peut-être que vous avez heurté la balance lorsque vous faisiez cette mesure, ou peut-être que votre partenaire de laboratoire est un idiot et que vous n’auriez jamais dû le laisser toucher à l’équipement. Qui sait ? Mais quelle que soit leur cause, les valeurs aberrantes sont ces points qui ne semblent pas « correspondre ».
Pourquoi une fois et demie la largeur de la boîte pour les valeurs aberrantes? Pourquoi cette valeur particulière marque-t-elle la différence entre les valeurs « acceptables » et « inacceptables »? Parce que, lorsque John Tukey inventait le tracé en boîte et moustache en 1977 pour afficher ces valeurs, il a choisi 1,5 × IQR comme ligne de démarcation pour les valeurs aberrantes. Cela a bien fonctionné, nous avons donc continué à utiliser cette valeur depuis. Si vous allez plus loin dans les statistiques, vous constaterez que cette mesure du caractère raisonnable, pour les données en forme de courbe en cloche, signifie qu’en général seulement peut-être jusqu’à environ un pour cent des données seront des valeurs aberrantes.
Vous pouvez utiliser le widget Mathway ci-dessous pour vous entraîner à trouver la plage interquartile, également appelée « H-spread » (ou ignorer le widget et continuer la leçon). Essayez l’exercice entré ou tapez votre propre exercice. Cliquez ensuite sur le bouton et faites défiler jusqu’à « Trouver la plage Interquartile (Propagation en H) » pour comparer votre réponse à celle de Mathway.
Veuillez accepter les cookies « préférences » afin d’activer ce widget.
(Cliquez sur « Appuyez pour afficher les étapes » pour accéder directement au site Mathway pour une mise à niveau payante.)
Une fois que vous êtes à l’aise de trouver l’IQR, vous pouvez passer à la localisation des valeurs aberrantes, le cas échéant.
-
Trouvez les valeurs aberrantes, le cas échéant, pour l’ensemble de données suivant :
10.2, 14.1, 14.4. 14.4, 14.4, 14.5, 14.5, 14.6, 14.7, 14.7, 14.7, 14.9, 15.1, 15.9, 16.4
Pour savoir s’il y a des valeurs aberrantes, je dois d’abord trouver l’IQR. Il y a quinze points de données, donc la médiane sera à la huitième position:
(15 + 1) ÷ 2 = 8
Alors Q2 = 14,6.
Il y a sept points de données de chaque côté de la médiane. Les deux moitiés sont :
10.2, 14.1, 14.4. 14.4, 14.4, 14.5, 14.5
…et :
14.7, 14.7, 14.7, 14.9, 15.1, 15.9, 16.4
Q1 est la quatrième valeur de la liste, étant la valeur intermédiaire de la première moitié de la liste; et Q3 est la douzième valeur, étant la th valeur moyenne de la seconde moitié de la liste :
Q1= 14,4
Q3=14,9
Alors l’IQR est donné par :
IQR=14,9–14,4 = 0,5
Les valeurs aberrantes seront tous les points inférieurs à Q1– 1,5 × IQR = 14,4 – 0,75 = 13,65 ou plus Q3 + 1,5 ×IQR = 14,9 + 0,75 = 15,65.
Alors les valeurs aberrantes sont à :
10,2, 15,9 et 16,4
Le contenu continue en dessous de
Les valeurs pour Q1–1,5×IQR et Q3+1.5×IQR sont les « clôtures » qui distinguent les valeurs « raisonnables » des valeurs aberrantes. Les valeurs aberrantes se trouvent à l’extérieur des clôtures.
Si votre affectation vous oblige à considérer non seulement les valeurs aberrantes mais aussi les « valeurs extrêmes », alors les valeurs pour Q1–1,5×IQR et Q3 + 1,5×IQR sont les clôtures « intérieures » et les valeurs pour Q1–3×IQR et Q3 + 3×IQR sont les clôtures « extérieures ».
Les valeurs aberrantes (marquées d’astérisques ou de points ouverts) se situent entre les clôtures intérieures et extérieures, et les valeurs extrêmes (marquées du symbole que vous n’avez pas utilisé pour les valeurs aberrantes) se trouvent à l’extérieur des clôtures extérieures.
Au fait, votre livre peut se référer à la valeur de « 1,5×IQR » comme étant une « étape ». Ensuite, les valeurs aberrantes seront les nombres situés entre un et deux pas des charnières, et la valeur extrême sera les nombres situés à plus de deux pas des charnières.
En regardant à nouveau l’exemple précédent, les clôtures extérieures seraient à 14,4-3×0,5 = 12,9 et 14,9 + 3×0,5 = 16,4. Puisque 16.4 est juste sur la clôture extérieure supérieure, cela serait considéré comme une valeur aberrante et non une valeur extrême. Mais 10,2 est entièrement en dessous de la clôture extérieure inférieure, donc 10,2 serait une valeur extrême.
Affilié
Affilié
Votre calculatrice graphique peut indiquer ou non si un tracé à moustaches comprend des valeurs aberrantes. Par exemple, le problème ci-dessus inclut les points 10.2, 15.9 et 16.4 comme valeurs aberrantes. Un paramètre de ma calculatrice graphique donne le tracé simple en boîte et moustaches qui utilise uniquement le résumé à cinq chiffres, de sorte que les valeurs aberrantes les plus éloignées sont affichées comme étant les points finaux des moustaches:

Un réglage différent de la calculatrice donne le tracé en boîte et moustaches avec les valeurs aberrantes spécialement marquées (dans ce cas, avec une simulation d’un point ouvert), et les moustaches allant uniquement jusqu’aux valeurs les plus élevées et les plus basses qui ne sont pas des valeurs aberrantes:

Ma calculatrice ne fait aucune distinction entre les valeurs aberrantes et les valeurs extrêmes. Le tien non plus. Consultez votre manuel d’utilisation dès maintenant, avant le prochain test.
Si vous utilisez votre calculatrice graphique pour vous aider avec ces tracés, assurez-vous de savoir quel paramètre vous êtes censé utiliser et ce que signifient les résultats, sinon la calculatrice peut vous donner une réponse parfaitement correcte mais « fausse ».
-
Trouvez les valeurs aberrantes et les valeurs extrêmes, le cas échéant, pour l’ensemble de données suivant, et tracez le tracé en boîte et moustache. Marquez toutes les valeurs aberrantes avec un astérisque et toutes les valeurs extrêmes avec un point ouvert.
21, 23, 24, 25, 29, 33, 49
Publicité
Pour trouver les valeurs aberrantes et extrêmes, je dois d’abord trouver l’IQR. Comme il y a sept valeurs dans la liste, la médiane est la quatrième valeur, donc :
Q2= 25
La première moitié de la liste est :
21, 23, 24
sodonc Q1 = 23; la seconde moitié est :
29, 33, 49
so donc Q3 = 33. Ensuite, l’IQR est donné par:
IQR=33 – 23=10
Les valeurs aberrantes seront toutes les valeurs ci-dessous :
23 – 1.5×10 = 23 – 15 = 8
…ou au-dessus :
33 + 1.5×10 = 33 + 15 = 48
Les valeurs extrêmes seront celles ci-dessous :
23 – 3×10 = 23 – 30 = -7
…ou au-dessus :
33 + 3×10 = 33 + 30 = 63
J’ai donc une valeur aberrante à 49 mais pas de valeurs extrêmes. Je n’aurai pas de moustache supérieure sur mon terrain car Q3 est également la valeur non aberrante la plus élevée. Donc mon intrigue ressemble à ceci:
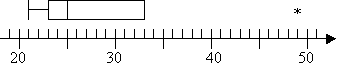
Il convient de noter que les méthodes, les termes et les règles décrits ci-dessus sont ce que j’ai enseigné et ce que j’ai le plus souvent vu enseigné. Cependant, votre cours peut avoir des règles spécifiques différentes, ou votre calculatrice peut effectuer des calculs légèrement différemment. Vous devrez peut-être faire preuve d’une certaine souplesse pour trouver les réponses spécifiques à votre programme d’études.
URL: https://www.purplemath.com/modules/boxwhisk3.htm
Page 1Page 2Page 3
Leave a Reply